Problem 254
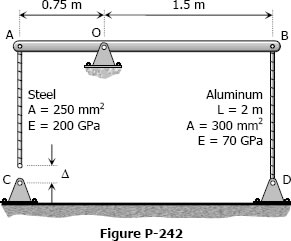
As shown in Fig. P-254, a rigid bar with negligible mass is pinned at O and attached to two vertical rods. Assuming that the rods were initially stress-free, what maximum load P can be applied without exceeding stresses of 150 MPa in the steel rod and 70 MPa in the bronze rod.
Problem 242
The assembly in Fig. P-242 consists of a light rigid bar AB, pinned at O, that is attached to the steel and aluminum rods. In the position shown, bar AB is horizontal and there is a gap, Δ = 5 mm, between the lower end of the steel rod and its pin support at C. Compute the stress in the aluminum rod when the lower end of the steel rod is attached to its support.
Problem 217
Solve Prob. 216 if rod AB is of steel, with E = 29 × 106 psi. Assume α = 45° and θ = 30°; all other data remain unchanged.
Problem 216
As shown in Fig. P-216, two aluminum rods AB and BC, hinged to rigid supports, are pinned together at B to carry a vertical load P = 6000 lb. If each rod has a cross-sectional area of 0.60 in.2 and E = 10 × 106 psi, compute the elongation of each rod and the horizontal and vertical displacements of point B. Assume α = 30° and θ = 30°.
Problem 121
Referring to Fig. P-121, compute the maximum force P that can be applied by the machine operator, if the shearing stress in the pin at B and the axial stress in the control rod at C are limited to 4000 psi and 5000 psi, respectively. The diameters are 0.25 inch for the pin, and 0.5 inch for the control rod. Assume single shear for the pin at B.
Problem 120
The members of the structure in Fig. P-120 weigh 200 lb/ft. Determine the smallest diameter pin that can be used at A if the shearing stress is limited to 5000 psi. Assume single shear.
Problem 119
Compute the shearing stress in the pin at B for the member supported as shown in Fig. P-119. The pin diameter is 20 mm.
Problem 118
A 200-mm-diameter pulley is prevented from rotating relative to 60-mm-diameter shaft by a 70-mm-long key, as shown in Fig. P-118. If a torque T = 2.2 kN·m is applied to the shaft, determine the width b if the allowable shearing stress in the key is 60 MPa.
