Solution to Problem 217 Axial Deformation

By Sine Law
$\dfrac{P_{AB}}{\sin 60^\circ} = \dfrac{6000}{\sin 75^\circ}$

$P_{AB} = 5379.45 \, \text{lb} \,$ (Tension)
 

 

$\dfrac{P_{BC}}{\sin 45^\circ} = \dfrac{6000}{\sin 75^\circ}$

$P_{BC} = 4392.30 \, \text{ lb}$   (Compression)
 

$\delta = \dfrac{PL}{AE}$

$\delta_{AB} = \dfrac{5379.45(10 \times 12)}{0.6(29 \times 10^6)} = 0.0371 \, \text{ inch}$   (lengthening)

$\delta_{BC} = \dfrac{4392.30(6 \times 12)}{0.6(10 \times 10^6)} = 0.0527 \, \text{ inch}$   (shortening)
 

From "Movement of B" diagram
DB = δ_AB = 0.0371 inch
BE = δ_BE = 0.0527 inch
δ_B = BB' = displacement of B
B' = final position of B after deformation
 

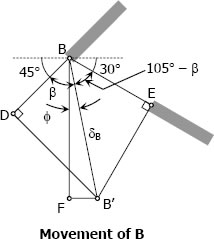Triangle BDB':
$\cos \beta = \dfrac{0.0371}{\delta_B}$

$\delta_B = \dfrac{0.0371}{\cos \beta}$
 

Triangle BEB':
$\cos (105^\circ - \beta) = \dfrac{0.0527}{\delta_B}$

$\delta_B = \dfrac{0.0527}{\cos (105^\circ - \beta)}$
 

$\delta_B = \delta_B$

$\dfrac{0.0371}{\cos \beta} = \dfrac{0.0527}{\cos (105^\circ - \beta)}$

$\dfrac{\cos 105^\circ \, \cos \beta + \sin 105^\circ \, \sin \beta}{\cos \beta} = 1.4205$

$-0.2588 + 0.9659 \tan \beta = 1.4205$

$\tan \beta = \dfrac{1.4205 + 0.2588}{0.9659}$

$\tan \beta = 1.7386$

$\beta = 60.1^\circ$
 

$\delta_B = \dfrac{0.0371}{\cos 60.1^\circ}$

$\delta_B = 0.0744 \, \text{inch}$
 

$\phi = (45^\circ + \beta) - 90^\circ$

$\phi = (45^\circ + 60.1^\circ) - 90^\circ$

$\phi = 15.1^\circ$
 

Triangle BFB':
$\delta_h = FB' = \delta_B \sin \phi = 0.0744 \sin 15.1^\circ$

$\delta_h = 0.0194 \, \text{inch}$

$\delta_h = 0.00162 \, \text{ ft}$       → horizontal displacement of B       answer
 

$\delta_v = BF = \delta_B \cos \phi = 0.0744 \cos 15.1^\circ$

$\delta_v = 0.07183 \, \text{inch}$

$\delta_v = 0.00598 \, \text{ft}$       → vertical displacement of B       answer