rigid support

Problem 325
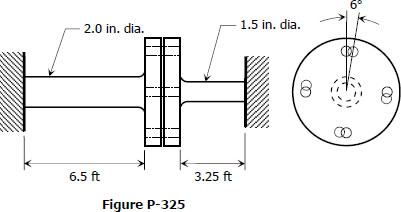
The two steel shaft shown in Fig. P-325, each with one end built into a rigid support have flanges rigidly attached to their free ends. The shafts are to be bolted together at their flanges. However, initially there is a 6° mismatch in the location of the bolt holes as shown in the figure. Determine the maximum shearing stress in each shaft after the shafts are bolted together. Use G = 12 × 10⁶ psi and neglect deformations of the bolts and flanges.
 

Problem 319
The compound shaft shown in Fig. P-319 is attached to rigid supports. For the bronze segment AB, the diameter is 75 mm, τ ≤ 60 MPa, and G = 35 GPa. For the steel segment BC, the diameter is 50 mm, τ ≤ 80 MPa, and G = 83 GPa. If a = 2 m and b = 1.5 m, compute the maximum torque T that can be applied.
 

Problem 246
Referring to the composite bar in Problem 245, what maximum axial load P can be applied if the allowable stresses are 10 ksi for aluminum and 18 ksi for steel.
 

Problem 245
The composite bar in Fig. P-245 is firmly attached to unyielding supports. Compute the stress in each material caused by the application of the axial load P = 50 kips.
 

Problem 244
A homogeneous bar with a cross sectional area of 500 mm² is attached to rigid supports. It carries the axial loads P₁ = 25 kN and P₂ = 50 kN, applied as shown in Fig. P-244. Determine the stress in segment BC. (Hint: Use the results of Prob. 243, and compute the reactions caused by P₁ and P₂ acting separately. Then use the principle of superposition to compute the reactions when both loads are applied.)
 

Problem 243
A homogeneous rod of constant cross section is attached to unyielding supports. It carries an axial load P applied as shown in Fig. P-243. Prove that the reactions are given by R₁ = Pb/L and R₂ = Pa/L.