Shearing Deformation

Shearing Deformation
Shearing forces cause shearing deformation. An element subject to shear does not change in length but undergoes a change in shape.

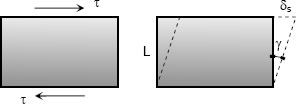
The change in angle at the corner of an original rectangular element is called the shear strain and is expressed as

$\gamma = \dfrac{\delta_s}{L}$

The ratio of the shear stress τ and the shear strain γ is called the modulus of elasticity in shear or modulus of rigidity and is denoted as G, in MPa.

$G = \dfrac{\tau}{\gamma}$

The relationship between the shearing deformation and the applied shearing force is

$\delta_s = \dfrac{VL}{A_s G} = \dfrac{\tau L}{G}$

where V is the shearing force acting over an area A_s.

Poisson's Ratio
When a bar is subjected to a tensile loading there is an increase in length of the bar in the direction of the applied load, but there is also a decrease in a lateral dimension perpendicular to the load. The ratio of the sidewise deformation (or strain) to the longitudinal deformation (or strain) is called the Poisson's ratio and is denoted by ν. For most steel, it lies in the range of 0.25 to 0.3, and 0.20 for concrete.

$\nu = -\dfrac{\varepsilon_y}{\varepsilon_x} = -\dfrac{\varepsilon_z}{\varepsilon_x}$

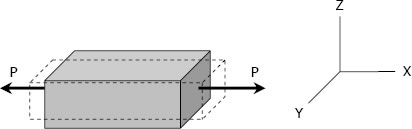
where ε_x is strain in the x-direction and ε_y and ε_z are the strains in the perpendicular direction. The negative sign indicates a decrease in the transverse dimension when ε_x is positive.

Biaxial Deformation
If an element is subjected simultaneously by tensile stresses, σ_x and σ_y, in the x and y directions, the strain in the x direction is σ_x/E and the strain in the y direction is σ_y/E. Simultaneously, the stress in the y direction will produce a lateral contraction on the x direction of the amount -ν ε_y or -ν σ_y/E. The resulting strain in the x direction will be

$\varepsilon_x = \dfrac{\sigma_x}{E} - \nu \dfrac{\sigma_y}{E}$ or $\sigma_x = \dfrac{(\varepsilon_x + \nu \varepsilon_y)E}{1 - \nu^2}$

and

$\varepsilon_y = \dfrac{\sigma_y}{E} - \nu \dfrac{\sigma_x}{E}$ or $\sigma_y = \dfrac{(\varepsilon_y + \nu \varepsilon_x)E}{1 - \nu^2}$

Triaxial Deformation
If an element is subjected simultaneously by three mutually perpendicular normal stresses σ_x, σ_y, and σ_z, which are accompanied by strains ε_x, ε_y, and ε_z, respectively,

$\varepsilon_x = \dfrac{1}{E} [ \, \sigma_x - \nu (\sigma_y + \sigma_z) \, ]$

$\varepsilon_y = \dfrac{1}{E} [ \, \sigma_y - \nu (\sigma_x + \sigma_z) \, ]$

$\varepsilon_z = \dfrac{1}{E} [ \, \sigma_z - \nu (\sigma_x + \sigma_y) \, ]$

Tensile stresses and elongation are taken as positive. Compressive stresses and contraction are taken as negative.

Relationship Between E, G, and ν
The relationship between modulus of elasticity E, shear modulus G and Poisson's ratio ν is:

$G = \dfrac{E}{2(1 + \nu)}$

Bulk Modulus of Elasticity or Modulus of Volume Expansion, K
The bulk modulus of elasticity K is a measure of a resistance of a material to change in volume without change in shape or form. It is given as

$K = \dfrac{E}{3(1 - 2\nu)} = \dfrac{\sigma}{\Delta V/V}$

where V is the volume and ΔV is change in volume. The ratio ΔV/V is called volumetric strain and can be expressed as

$\dfrac{\Delta V}{V} = \dfrac{\sigma}{K} = \dfrac{3(1 - 2\nu)}{E}$

Navigation

Recent comments