Problem 227
A 150-mm-long bronze tube, closed at its ends, is 80 mm in diameter and has a wall thickness of 3 mm. It fits without clearance in an 80-mm hole in a rigid block. The tube is then subjected to an internal pressure of 4.00 MPa. Assuming ν = 1/3 and E = 83 GPa, determine the tangential stress in the tube.
Problem 226
A 2-in.-diameter steel tube with a wall thickness of 0.05 inch just fits in a rigid hole. Find the tangential stress if an axial compressive load of 3140 lb is applied. Assume ν = 0.30 and neglect the possibility of buckling.
Problem 225
A welded steel cylindrical drum made of a 10-mm plate has an internal diameter of 1.20 m. Compute the change in diameter that would be caused by an internal pressure of 1.5 MPa. Assume that Poisson's ratio is 0.30 and E = 200 GPa.
Shearing Deformation
Shearing forces cause shearing deformation. An element subject to shear does not change in length but undergoes a change in shape.
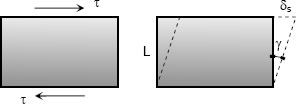
The change in angle at the corner of an original rectangular element is called the shear strain and is expressed as
The ratio of the shear stress τ and the shear strain γ is called the modulus of elasticity in shear or modulus of rigidity and is denoted as G, in MPa.
The relationship between the shearing deformation and the applied shearing force is
where V is the shearing force acting over an area As.
