Solution to Problem 205 Axial Deformation

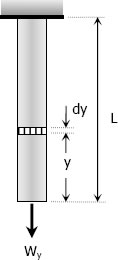
$\delta = \dfrac{PL}{AE}$

From the figure:
$\delta = d\delta$

$P = W_y = (\rho Ay)g$

$L = dy$

 

Thus,
$d\delta = \dfrac{(\rho Ay)g \, dy}{AE}$

$\delta = \dfrac{\rho g}{E} \displaystyle \int_0^L y \, dy = \dfrac{\rho g}{E} \left[ \dfrac{y^2}{2} \right]_0^L$

$\delta = \dfrac{\rho g}{2E} [ \, L^2 - 0^2 \, ]$

$\delta = \rho gL^2 / 2E$           (okay!)
 

Given the total mass M
$\rho = M/V = M/AL$

$\delta = \dfrac{\rho gL^2}{2E} = \dfrac{\dfrac{M}{AL} \cdot gL^2}{2E}$

$\delta = \dfrac{MgL}{2AE}$           (okay!)
 

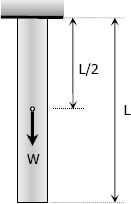Another Solution:
$\delta = \dfrac{PL}{AE}$
 

Where:
$P = W = (\rho AL)g$

$L = \frac{1}{2}L$

 

Thus,
$\delta = \dfrac{[(\rho AL)g](\frac{1}{2}L)}{AE}$

$\delta = \rho gL^2 / 2E$           (okay!)
 

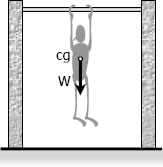For you to feel the situation, position yourself in pull-up exercise with your hands on the bar and your body hang freely above the ground. Notice that your arms suffer all your weight and your lower body fells no stress (center of weight is approximately just below the chest). If your body is the bar, most elongation will occur at the upper half of it.