The Right Circular Cone
Any cone with circular right section is a circular cone. Right circular cone is a circular cone whose axis is perpendicular to its base.
- Read more about The Right Circular Cone
- Log in or register to post comments
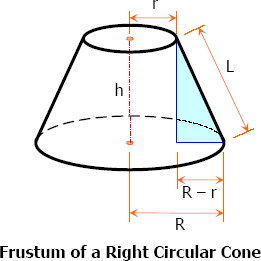
Frustum of a Right Circular Cone
Frustum of a right circular cone is that portion of right circular cone included between the base and a section parallel to the base not passing through the vertex.
- Read more about Frustum of a Right Circular Cone
- Log in or register to post comments
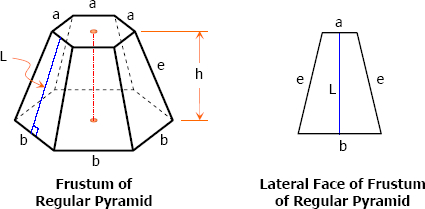
Frustum of a Regular Pyramid
Frustum of a regular pyramid is a portion of right regular pyramid included between the base and a section parallel to the base.
- Read more about Frustum of a Regular Pyramid
- Log in or register to post comments
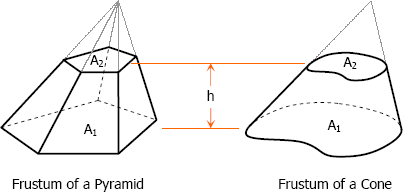
Frustums
Frustum of a pyramid (or cone) is a portion of pyramid (or cone) included between the base and the section parallel to the base not passing through the vertex.
- Read more about Frustums
- Log in or register to post comments
The Cone
Cone
The surface generated by a moving straight line (generator) which always passes through a fixed point (vertex) and always intersects a fixed plane curve (directrix) is called conical surface. Cone is a solid bounded by a conical surface whose directrix is a closed curve, and a plane which cuts all the elements. The conical surface is the lateral area of the cone and the plane which cuts all the elements is the base of the cone.
- Read more about The Cone
- Log in or register to post comments
Similar Figures
Two surfaces or solids are similar if any two corresponding sides or planes are proportional.
- Read more about Similar Figures
- Log in or register to post comments
Solution to Problem 670 | Deflections in Simply Supported Beams
Problem 670
Determine the value of EIδ at the left end of the overhanging beam shown in Fig. P-670.

Solution to Problem 669 | Deflections in Simply Supported Beams
Problem 669
Compute the value of EIδ midway between the supports of the beam shown in Fig. P-669.

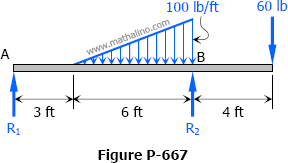
Solution to Problem 668 | Deflections in Simply Supported Beams
Problem 668
For the beam shown in Fig. P-668, compute the value of P that will cause the tangent to the elastic curve over support R2 to be horizontal. What will then be the value of EIδ under the 100-lb load?


Recent comments