Frustum of a Regular Pyramid

Frustum of a regular pyramid is a portion of right regular pyramid included between the base and a section parallel to the base.

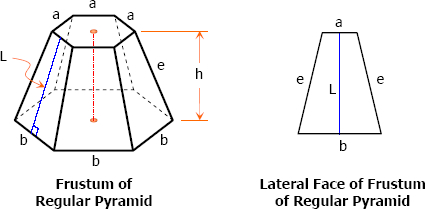
Properties of a Frustum of Regular Pyramid

The slant height of a frustum of a regular pyramid is the altitude of the face.
The lateral edges of a frustum of a regular pyramid are equal, and the faces are equal isosceles trapezoids.
The bases of a frustum of a regular pyramid are similar regular polygons. If these polygons become equal, the frustum will become prism.

Elements of a Frustum of Regular Pyramid
a = upper base edge
b = lower base edge
e = lateral edge
h = altitude
L = slant height
A₁ = area of lower base
A₂ = area of upper base
n = number of lower base edges

Formulas for Frustum of a Regular Pyramid

Area of Bases, A₁ and A₂
See the formulas of regular polygon for the formula of A₁ and A₂

Volume

$V = \frac{1}{3}\left( A_1 + A_2 + \sqrt{A_1A_2} \right)h$

See the derivation of formula for volume of a frustum.

Lateral Area, A_L
The lateral area of frustum of regular pyramid is equal to one-half the sum of the perimeters of the bases multiplied by the slant height.

$A_L = \frac{1}{2} n (a + b)L$

The relationship between slant height L, lower base edge b, upper base edge a, and lateral edge e, of the frustum of regular pyramid is given by

$(b - a)^2 + 4L^2 = 4e^2$

Navigation

Recent comments