Frustum of a Regular Pyramid
Frustum of a regular pyramid is a portion of right regular pyramid included between the base and a section parallel to the base.
- Read more about Frustum of a Regular Pyramid
- Log in or register to post comments
Solids for Which Volume = Mean of Base Areas times Altitude
Frustums
Frustum of a pyramid (or cone) is a portion of pyramid (or cone) included between the base and the section parallel to the base not passing through the vertex.
$V = \frac{1}{3}\left( A_1 + A_2 + \sqrt{A_1A_2} \right)h$
- Read more about Frustums
- Log in or register to post comments
Derivation of formula for volume of a frustum of pyramid/cone
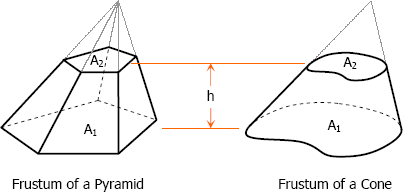
Frustum of a pyramid and frustum of a cone
The formula for frustum of a pyramid or frustum of a cone is given by
$V = \dfrac{h}{3} \left[ \, A_1 + A_2 + \sqrt{A_1A_2} \, \right]$
Where:
h = perpendicular distance between A1 and A2 (h is called the altitude of the frustum)
A1 = area of the lower base
A2 = area of the upper base
Note that A1 and A2 are parallel to each other.