Derivation of formula for volume of a frustum of pyramid/cone

Frustum of a pyramid and frustum of a cone
 

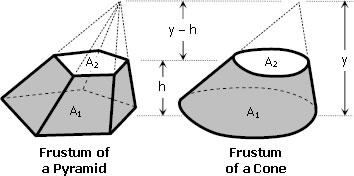
The formula for frustum of a pyramid or frustum of a cone is given by
 

Where:
h = perpendicular distance between A₁ and A₂ (h is called the altitude of the frustum)
A₁ = area of the lower base
A₂ = area of the upper base
Note that A₁ and A₂ are parallel to each other.
 

Derivation:
$V_1 = \frac{1}{3}A_1 y$

$V_2 = \frac{1}{3}A_2 (y - h)$
 

$V = V_1 - V_2 = \frac{1}{3}A_1 y - \frac{1}{3}A_2 (y - h)$

$V = \frac{1}{3}A_1 y - \frac{1}{3}A_2 y + \frac{1}{3}A_2 h$

$V = \frac{1}{3} \, \left[ \, (A_1 - A_2) y + A_2 h \right]$   →   Equation (1)
 

By similar solids (Click here for more information about Similar Solids):
$\dfrac{A_2}{A_1} = \left( \dfrac{y - h}{y} \right)^2$

$\sqrt{\dfrac{A_2}{A_1}} = 1 - \dfrac{h}{y}$

$\dfrac{h}{y} = 1 - \sqrt{\dfrac{A_2}{A_1}} = 1 - \dfrac{\sqrt{A_2}}{\sqrt{A_1}}$

$\dfrac{h}{y} = \dfrac{\sqrt{A_1} - \sqrt{A_2}}{\sqrt{A_1}}$

$\dfrac{y}{h} = \dfrac{\sqrt{A_1}}{\sqrt{A_1} - \sqrt{A_2}}$

$y = \dfrac{\sqrt{A_1}}{\sqrt{A_1} - \sqrt{A_2}}\,h = \left( \dfrac{\sqrt{A_1}}{\sqrt{A_1} - \sqrt{A_2}} \, \times \, \dfrac{\sqrt{A_1} + \sqrt{A_2}}{\sqrt{A_1} + \sqrt{A_2}}\right)\,h$

$y = \dfrac{A_1 + \sqrt{A_1A_2}}{A_1 - A_2}\,h$
 

Substitute y to Equation (1),
$V = \frac{1}{3} \, \left[ \, (A_1 - A_2) \left( \dfrac{A_1 + \sqrt{A_1A_2}}{A_1 - A_2}\,h \right) + A_2 h \right]$

$V = \frac{1}{3} \, \left[ \, (A_1 + \sqrt{A_1A_2})h + A_2 h \, \right]$

$V = \frac{1}{3} \, \left[ \, A_1 + \sqrt{A_1A_2} + A_2 \, \right] \, h$