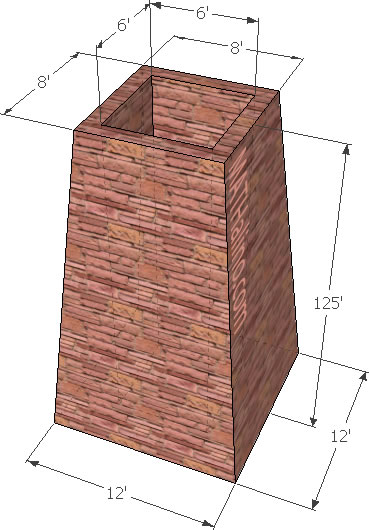
041 Review Problem - Weight capacity of industrial soap kettle
Problem 41
Soap kettles used in the commercial manufacture of soap are as a rule large cylindrical vats, 50,000 lb. or more of soap being made in a single beating. Find the capacity of such a kettle having an inside diameter of 18 ft and an altitude of 30 ft. if soap weighs 70 lb. per cu. ft.