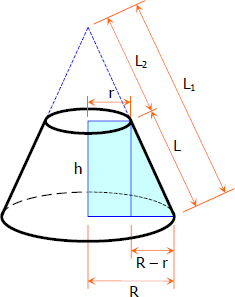
Derivation of Formula for Lateral Area of Frustum of a Right Circular Cone

The lateral area of frustum of a right circular cone is given by the formula
 

 

where
R = radius of the lower base
r = radius of the upper base
L = length of lateral side
 

Derivation of Formula
Lateral area of right circular cone is the difference of the areas of sectors of a circle of radii L₁ and L₂ and common central angle θ. See the figure below
 

 

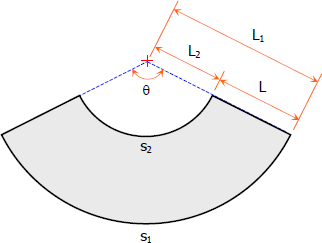
By ratio and proportion:
$\dfrac{L_1}{R} = \dfrac{L}{R - r}$

$L_1 = \dfrac{RL}{R - r}$
 

From the figure:
$L_2 = L_1 - L$

$L_2 = \dfrac{RL}{R - r} - L$

$L_2 = \dfrac{RL - (R - r)L}{R - r}$

$L_2 = \dfrac{rL}{R - r}$

 
The length of arc is the circumference of the base:
$s_1 = 2\pi R$

$s_2 = 2\pi r$
 

From the figure:
$A = \frac{1}{2}s_1 \, L_1 - \frac{1}{2}s_2 \, L_2$

$A = \frac{1}{2}(2\pi R) \left( \dfrac{RL}{R - r} \right)- \frac{1}{2}(2\pi r) \left( \dfrac{rL}{R - r} \right)$

$A = \dfrac{\pi R^2 L}{R - r} - \dfrac{\pi r^2 L}{R - r}$

$A = \dfrac{\pi R^2 L - \pi r^2 L}{R - r}$

$A = \dfrac{\pi (R^2 - r^2) \, L}{R - r}$

$A = \dfrac{\pi (R - r)(R + r) \, L}{R - r}$