Derivation of Formula for Total Surface Area of the Sphere by Integration

The total surface area of the sphere is four times the area of great circle. To know more about great circle, see properties of a sphere. Given the radius r of the sphere, the total surface area is
 

 

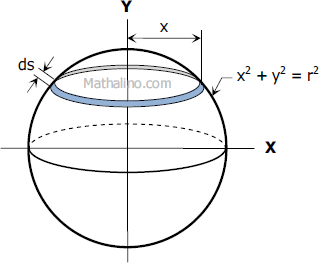
From the figure, the area of the strip is
$dA = 2\pi \, x \, ds$
 

Where ds is the length of differential arc which is given by
$ds = \sqrt{1 + \left( \dfrac{dy}{dx} \right)^2} \, dx = \sqrt{1 + \left( \dfrac{dx}{dy} \right)^2} \, dy$
 

 

See Length of Arc in Integral Calculus for more information about ds.
 

The total area of the sphere is equal to twice the sum of the differential area dA from 0 to r.
$\displaystyle A = 2 \left( \int_0^r 2\pi \, x \, ds \right)$

$\displaystyle A = 4\pi \int_0^r x \sqrt{1 + \left( \dfrac{dy}{dx} \right)^2} \, dx$
 

From the figure,
$x^2 + y^2 = r^2$

$y = \sqrt{r^2 - x^2}$

$\dfrac{dy}{dx} = \dfrac{-2x}{2\sqrt{r^2 - x^2}}$

$\dfrac{dy}{dx} = \dfrac{-x}{\sqrt{r^2 - x^2}}$

$\left( \dfrac{dy}{dx} \right)^2 = \dfrac{x^2}{r^2 - x^2}$
 

Thus,
$\displaystyle A = 4\pi \int_0^r x \sqrt{1 + \dfrac{x^2}{r^2 - x^2}} \, dx$

$\displaystyle A = 4\pi \int_0^r x \sqrt{\dfrac{(r^2 - x^2) + x^2}{r^2 - x^2}} \, dx$

$\displaystyle A = 4\pi \int_0^r x \sqrt{\dfrac{r^2}{r^2 - x^2}} \, dx$
 

Let
x = r sin θ
dx = r cos θ dθ

When x = 0, θ = 0
When x = r, θ = π/2
 

Thus,
$\displaystyle A = 4\pi \int_0^{\pi/2} r \sin \theta \sqrt{\dfrac{r^2}{r^2 - r^2 \sin^2 \theta}} \, (r \cos \theta \, d\theta)$

$\displaystyle A = 4\pi \int_0^{\pi/2} r^2 \sin \theta \cos \theta\sqrt{\dfrac{r^2}{r^2(1 - \sin^2 \theta)}} \, d\theta$

$\displaystyle A = 4\pi r^2 \int_0^{\pi/2} \sin \theta \cos \theta\sqrt{\dfrac{1}{\cos^2 \theta}} \, d\theta$

$\displaystyle A = 4\pi r^2 \int_0^{\pi/2} \sin \theta \cos \theta \left( \dfrac{1}{\cos \theta} \right) \, d\theta$

$\displaystyle A = 4\pi r^2 \int_0^{\pi/2} \sin \theta \, d\theta$

$A = 4\pi r^2 \bigg[-\cos \theta \bigg]_0^{\pi/2}$

$A = 4\pi r^2 \bigg[-\cos \frac{1}{2}\pi + \cos 0 \bigg]$

$A = 4\pi r^2 \bigg[ -0 + 1 \bigg]$

$A = 4\pi r^2$           okay!