The Distance the Particle Travels with Given Position Function x(t) = t^4 - 8t^2
Problem
Given the position function x(t) = t4 - 8t2, find the distance that the particle travels at t = 0 to t = 4.
| A. 160 | C. 140 |
| B. 150 | D. 130 |
Length of Arc
Perimeter of the curve $r = 4(1 + \sin \theta)$ by integration
Problem
What is the perimeter of the curve r = 4(1 + sin θ)?
The answer is 32 units. For detailed solution, follow the link by clicking on the figure.
Length of Arc in Polar Plane | Applications of Integration
The length of arc in polar plane is given by the formula:
$\displaystyle s = \int_{\theta_1}^{\theta_2} \sqrt{r^2 + \left( \dfrac{dr}{d\theta} \right)^2} ~ d\theta$
The formula above is derived in two ways.
Length of Arc in XY-Plane | Applications of Integration
The length of arc in rectangular coordinates is given by the following formulas:
$\displaystyle s = \int_{x_1}^{x_2} \sqrt{1 + \left( \dfrac{dy}{dx} \right)^2} \, dx$ and $\displaystyle s = \int_{y_1}^{y_2} \sqrt{1 + \left(\dfrac{dx}{dy} \right)^2} \, dy$
See the derivations here: http://www.mathalino.com/reviewer/integral-calculus/length-arc-xy-plane…
Angle between two chords
Problem
Chords AB and AC are drawn on a circle of radius 10 inches. Find the angle between the chords if the arc BAC is 28 inches long.
- Read more about Angle between two chords
- Log in to post comments
Cycloid: equation, length of arc, area
Problem
A circle of radius r rolls along a horizontal line without skidding.
- Find the equation traced by a point on the circumference of the circle.
- Determine the length of one arc of the curve.
- Calculate the area bounded by one arc of the curve and the horizontal line.
- Read more about Cycloid: equation, length of arc, area
- Log in to post comments
717 Symmetrical Arcs and a Line | Centroid of Composite Line
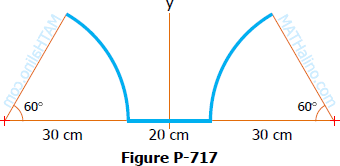
Problem 717
Locate the centroid of the bent wire shown in Fig. P-717. The wire is homogeneous and of uniform cross-section.
Derivation of Formula for Total Surface Area of the Sphere by Integration
The total surface area of the sphere is four times the area of great circle. To know more about great circle, see properties of a sphere. Given the radius r of the sphere, the total surface area is