Length of Arc in XY-Plane | Applications of Integration

 

 

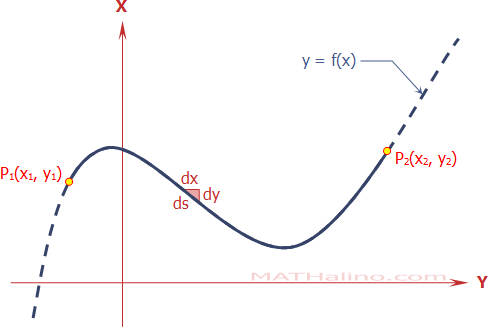
Apply Pythagorean theorem to the triangular strip shown in the figure:
$(ds)^2 = (dx)^2 + (dy)^2$   ←   Equation (1)
 

length-of-arc-xy-plane.jpg

 

Divide both sides of Equation (1) by (dx)2
$\dfrac{(ds)^2}{(dx)^2} = \dfrac{(dx)^2}{(dx)^2} + \dfrac{(dy)^2}{(dx)^2}$

$\left( \dfrac{ds}{dx} \right)^2 = 1 + \left( \dfrac{dy}{dx} \right)^2$

$\dfrac{ds}{dx} = \sqrt{1 + \left( \dfrac{dy}{dx} \right)^2}$

$ds = \sqrt{1 + \left( \dfrac{dy}{dx} \right)^2} \, dx$
 

Integrate both sides

$\displaystyle s = \int_{x_1}^{x_2} \sqrt{1 + \left( \dfrac{dy}{dx} \right)^2} \, dx$

 

Divide both sides of Equation (1) by (dy)2
$\dfrac{(ds)^2}{(dy)^2} = \dfrac{(dx)^2}{(dy)^2} + \dfrac{(dy)^2}{(dy)^2}$

$\left( \dfrac{ds}{dy} \right)^2 = \left( \dfrac{dx}{dy} \right)^2 + 1$

$\dfrac{ds}{dy} = \sqrt{\left( \dfrac{dx}{dy} \right)^2 + 1}$

$ds = \sqrt{\left( \dfrac{dx}{dy} \right)^2 + 1} ~ dy$

 

Integrate both sides

$\displaystyle s = \int_{y_1}^{y_2} \sqrt{\left( \dfrac{dx}{dy} \right)^2 + 1} ~ dy$

 

Tags
Rectangular Coordinates
Length of Arc
Derivation of Formula