Plane Areas in Polar Coordinates | Applications of Integration
The fundamental equation for finding the area enclosed by a curve whose equation is in polar coordinates is...
$\displaystyle A = \frac{1}{2}{\int_{\theta_1}^{\theta_2}} r^2 \, d\theta$
Where θ1 and θ2 are the angles made by the bounding radii.
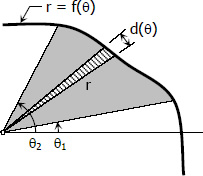
The formula above is based on a sector of a circle with radius r and central angle dθ. Note that r is a polar function or r = f(θ). See figure above.