Volumes of Solids of Revolution | Applications of Integration

Solids of Revolution by Integration

The solid generated by rotating a plane area about an axis in its plane is called a solid of revolution. The volume of a solid of revolution may be found by the following procedures:
 

Circular Disk Method

The strip that will revolve is perpendicular to the axis of revolution. In this method, the axis of rotation may or may not be part of the boundary of the plane area that is being revolved.
 

Using Horizontal Strip
 

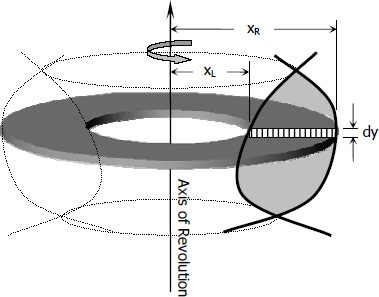
Solids of Revolution by Integration

 

The disk as shown in the figure has an outer radius of xR, a hole of radius xL, and thickness dy. The differential volume is therefore π xR2 dy - π xL2 dy and the total volume is...
 

$\displaystyle V = \pi {\int_{y_1}^{y_2}} ({x_R}^2 - {x_L}^2) \, dy$

 

The integration involved is in variable y since the derivative is dy, xR and xL therefore must be expressed in terms of y. If the axis of revolution is part of the boundary of the plane area that is being revolved, xL = 0, and the equation reduces to...
 

$\displaystyle V = \pi {\int_{y_1}^{y_2}} {x_R}^2 \, dy$

 

Using Vertical Strip
From the figure shown below, the volume can be found by the formula...
 

$\displaystyle V = \pi {\int_{x_1}^{x_2}} ({y_U}^2 - {y_L}^2) \, dx$

 

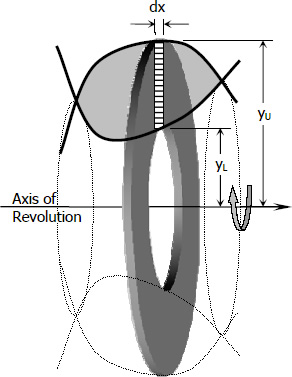
solids-of-revolution-circular-disk-method-vertical-strip.jpg

 

If yL = 0, we have
 

$\displaystyle V = \pi {\int_{x_1}^{x_2}} {y_U}^2 \, dx$$

 

Where yU and yL are functions of x.
 

Cylindrical Shell Method

The strip that will revolve is parallel to the axis of revolution. The volume of revolution is obtained by taking the limit of the sum of cylindrical shell elements, each of which is equal in volume to the mean circumference times the height times the thickness.
 

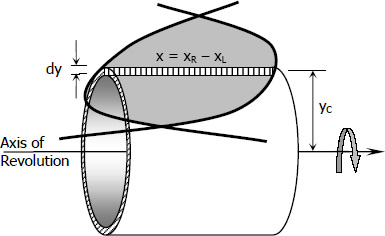
Using Horizontal Strip
 

solids-of-revolution-cylindrical-shell-method-horizontal-strip.jpg

 

$\displaystyle V = 2\pi {\int_{y_1}^{y_2}} y_C(x_R - x_L) \, dy$

 

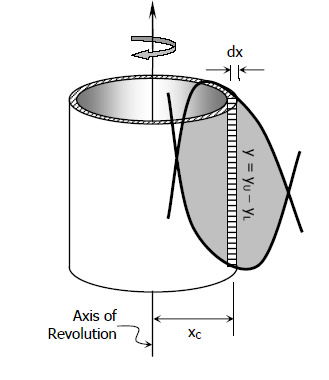
Using Vertical Strip
 

solids-of-revolution-cylindrical-shell-method-vertical-strip.jpg

 

$\displaystyle V = 2\pi {\int_{x_1}^{x_2}} x_C(y_U - x_L) \, dx$

 

Tags
Volume
solids of revolution
Volume by Integration
cylindrical shell method
circular disk method