polar coordinates

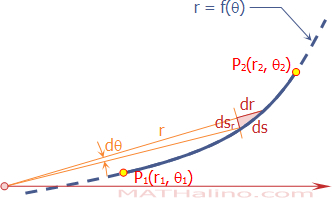
In Polar Coordinate System, the references are a fixed point and a fixed line. The fixed point is called the pole and the fixed line is called the polar axis. The location of a point is expressed according to its distance from the pole and its angle from the polar axis. The distance is denoted by r and the angle by θ.

The length of arc in polar plane is given by the formula:

The formula above is derived in two ways.
 

Find the area enclosed by four-leaved rose r = a cos 2θ.
 

The fundamental equation for finding the area enclosed by a curve whose equation is in polar coordinates is...