Integration of Polar Area
06 Area Within the Curve r^2 = 16 cos θ
Example 6
What is the area within the curve r2 = 16 cos θ?
- Read more about 06 Area Within the Curve r^2 = 16 cos θ
- Log in to post comments
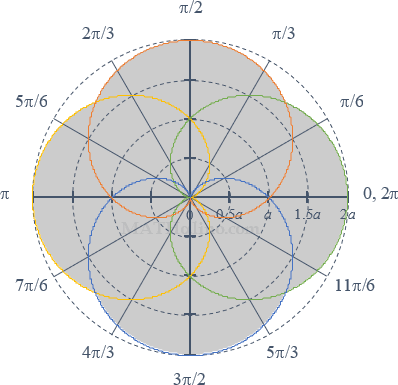
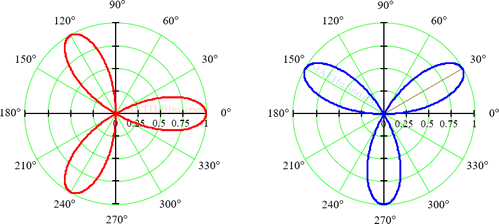
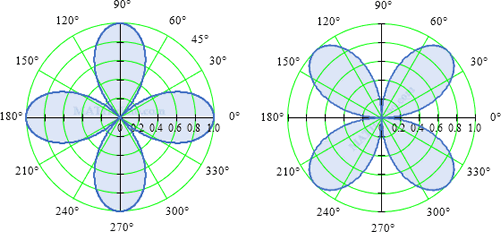
05 Area Enclosed by Four-Leaved Rose r = a cos 2θ
Find the area enclosed by four-leaved rose r = a cos 2θ.
04 Area of the Inner Loop of the Limacon r = a(1 + 2 cos θ)
Example 4
Find the area of the inner loop of the limacon r = a(1 + 2 cos θ).
03 Area Inside the Cardioid r = a(1 + cos θ) but Outside the Circle r = a
Example 3
Find the area inside the cardioid r = a(1 + cos θ) but outside the circle r = a.
02 Area Bounded by the Lemniscate of Bernoulli r^2 = a^2 cos 2θ
Example 2
Find the area bounded by the lemniscate of Bernoulli r2 = a2 cos 2θ.
Plane Areas in Polar Coordinates | Applications of Integration
The fundamental equation for finding the area enclosed by a curve whose equation is in polar coordinates is...
$\displaystyle A = \frac{1}{2}{\int_{\theta_1}^{\theta_2}} r^2 \, d\theta$