Conical Frustum

Problem 39
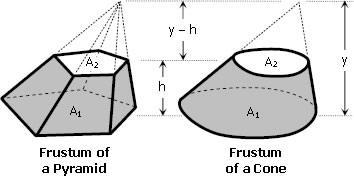
A grain elevator in the form of a frustum of a right circular cone is 24 ft. high, and the radii of its bases are 10 ft. and 5 ft., respectively; how many bushels of wheat will it hold if 1-1/4 cu. ft. equals 1 bu.?
 

Problem 38
A log 18 ft. long is 2 ft. in diameter at the top end and 3 ft. in diameter at the butt end.
 

1. How many cubic feet of wood does the log contain?
2. How many cubic feet are there in the largest piece of timber of square cross section that can be cut from the log?
3. How many cubic feet are in the largest piece of square timber of the same size throughout its whole length?
4. How many board feet does the piece of timber in (c), a board foot being equivalent to a board 1 ft. square and 1 in. thick?

Hint: In (b) the larger end is the square ABCD. What is the smaller end? In (c) one end is the square EFGH. What is the other end?

Problem 32
A coffee pot is 5 in. deep, 4-1/2 in. in diameter at the top, and 5-3/4 in. in diameter at the bottom. How many cups of coffee will it hold if 6 cups equal 1 quart? Answer to the nearest whole number.
 

Problem 22
How many square feet of tin are required to make a funnel, if the diameters of the top and bottom are 28 in. and 14 in., respectively, and the height is 24 in.?
 

Problem 13
The accompanying figure represents the longitudinal view of a Venturi meter, a device designed to measure the flow of water in pipes. If the throat of the of the meter is 6 in. long and has an inside diameter of 4 in., find the volume of water in the meter which is used in 12-in. pipe line if the altitudes of the tapering parts are in the ratio 1:3 and the smaller altitude measures 12 in.
 

Frustum of a pyramid and frustum of a cone
 

The formula for frustum of a pyramid or frustum of a cone is given by
 

Where:
h = perpendicular distance between A₁ and A₂ (h is called the altitude of the frustum)
A₁ = area of the lower base
A₂ = area of the upper base
Note that A₁ and A₂ are parallel to each other.