Problem
What height of mercury column will cause a pressure of 680 kPa? What is the equivalent height of water column?
 

Problem
Take sea water to be 3% heavier than fresh water and assume it is incompressible. What is the pressure, in metric ton per square meter, at 3.22 km below the surface of the ocean if fresh water weighs 9.79 kN/m³?
 

Problem
Determine the pressure on the face of a dam at a point 12 m below the water surface, in (a) kilo Pascal gauge; (b) kilogram per square meter gauge; (c) kilo Pascal absolute; (d) pounds per square foot gauge; (e) pounds per square inch gauge; and (e) pounds per square inch absolute.
 

Problem
Determine the pressure in a vessel of mercury, specific gravity 13.6, at a point 20 cm below the surface. Express the answer in N/m².
 

Consider two points 1 and 2 lie in the ends of fluid prism having a cross-sectional area dA and length L. The difference in elevation between these two points is h as shown in Figure 02 below. The fluid is at rest and its surface is free. The prism is therefore in equilibrium and all forces acting on it sums up to zero.
 

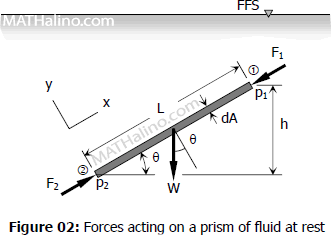
Note: FFS stands for Free Fluid Surface which refers to fluid surface subject to zero gauge pressure.
 

Unit Pressure
Unit pressure or simply called pressure is the amount of force exerted by a fluid distributed uniformly over a unit area.
 

If the unit pressure is not uniform over the unit area, it can be expressed as the sum of differential pressure.
 

Blaise Pascal (1623 – 1662)

Since fluid at rest cannot resist shearing stress, pressure is always at right angle to the area where it is acting. It is also worthy to note that the total hydrostatic force F = pA, which can be found by cross multiplication.
 

Situation
The helical spring shown is axially loaded with a compression force P equal to 5 kN. The mean diameter of the spring is 100 mm and the wire used is 10 mm as indicated in the figure.

1. What is the shear stress at A?
2. What is the shear stress at B?
3. On diameter AB, locate the point of zero stress measured from C.

 Problem 908
A punch press has the cast steel frame shown in Figure P-908. Determine the greatest force P that can be exerted at the jaws of the punch without exceeding a stress of 18 ksi at section A-B. The properties of the area are as shown and 1-1 is the centroidal axis.
 

Problem 907
Determine the largest load P that can be supported by the circular steel bracket shown in Figure P-907 if the normal stress on section A-B is limited to 80 MPa.
 

Problem 906
For the 2-in. by 6-in. wooden beam shown in Fig. P-906. Determine the normal stress at A and B. Are these the points of maximum normal stress? If not, where are they located and what are their values?