$\Sigma M_A = 0$
$12R_D + 4800 = 3(2000)$
$R_D = 100 \, \text{lb}$
$\Sigma M_D = 0$
$12R_A = 9(2000) + 4800$
$R_A = 1900 \, \text{lb}$
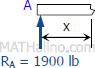Segment AB:
$V_{AB} = 1900 \, \text{lb}$
$M_{AB} = 1900x \, \text{lb}\cdot\text{ft}$
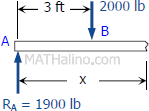Segment BC:
$V_{BC} = 1900 - 2000$
$V_{BC} = -100 \, \text{lb}$
$M_{BC} = 1900x - 2000(x - 3)$
$M_{BC} = 1900x - 2000x + 6000$
$M_{BC} = -100x + 6000 \, \text{lb}\cdot\text{ft}$
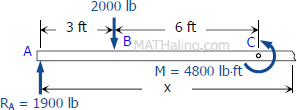Segment CD:
$V_{CD} = 1900 - 2000$
$V_{CD} = -100 \, \text{lb}$
$M_{CD} = 1900x - 2000(x - 3) - 4800$
$M_{CD} = 1900x - 2000x + 6000 - 4800$
$M_{CD} = -100x + 1200 \, \text{lb}\cdot\text{ft}$
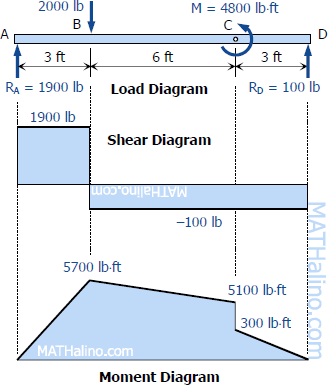To draw the shear diagram:
- At segment AB, the shear is uniformly distributed at 1900 lb.
- A shear of -100 lb is uniformly distributed over segments BC and CD.
To draw the Moment Diagram:
- MAB = 1900x is linear; at x = 0, MAB = 0; at x = 3 ft, MAB = 5700 lb·ft.
- For segment BC, MBC = -100x + 6000 is linear; at x = 3 ft, MBC = 5700 lb·ft; at x = 9 ft, MBC = 5100 lb·ft.
- MCD = -100x + 1200 is again linear; at x = 9 ft, MCD = 300 lb·ft; at x = 12 ft, MCD = 0.
