Solution to Problem 420 | Shear and Moment Diagrams

$w = 2500 \, \text{lb/ft}$
 

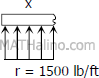
$\Sigma F_V = 0$

$R = W$

$20r = 30(1000)$

$r = 1500 \, \text{lb/ft}$
 

First segment (from 0 to 4 ft from left):
$V_1 = 1500x$
$M_1 = 1500x(x/2)$
$M_1 = 750x^2$
 

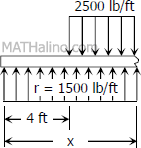Second segment (from 4 ft to mid-span):
$V_2 = 1500x - 2500(x - 4)$

$V_2 = 10000 - 1000x$
 

$M_2 = 1500x(x/2) - 2500(x - 4)(x - 4)/2$

$M_2 = 750x^2 - 1250(x - 4)^2$
 

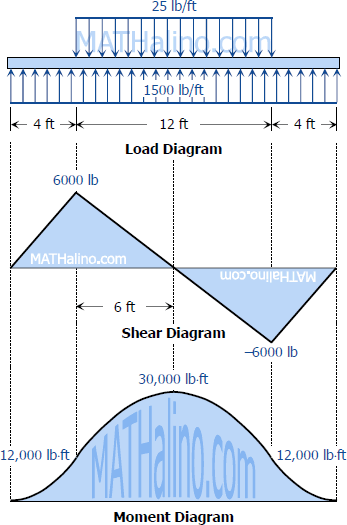To draw the Shear Diagram:

1. For the first segment, V₁ = 1500x is linear; at x = 0, V₁ = 0; at x = 4 ft, V₁ = 6000 lb.
2. For the second segment, V₂ = 10000 - 1000x is also linear; at x = 4 ft, V₁ = 6000 lb; at mid-span, x = 10 ft, V₁ = 0.
3. For the next half of the beam, the shear diagram can be accomplished by the concept of symmetry.

To draw the Moment Diagram:

1. For the first segment, M₁ = 750x² is a second degree curve, an open upward parabola; at x = 0, M₁ = 0; at x = 4 ft, M₁ = 12000 lb·ft.
2. For the second segment, M₂ = 750x² - 1250(x - 4)² is a second degree curve, an downward parabola; at x = 4 ft, M₂ = 12000 lb·ft; at mid-span, x = 10 ft, M₂ = 30000 lb·ft.
3. The next half of the diagram, from x = 10 ft to x = 20 ft, can be drawn by using the concept of symmetry.