Conjugate Beam Method | Beam Deflection
Deflection on real beam = Moment on conjugate beam
Properties of Conjugate Beam

Engr. Christian Otto Mohr
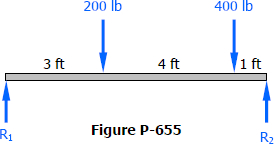
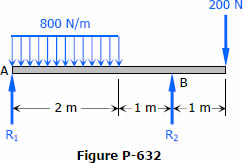
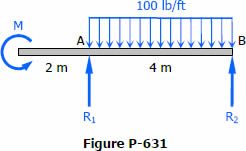
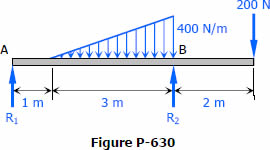
- The length of a conjugate beam is always equal to the length of the actual beam.
- The load on the conjugate beam is the M/EI diagram of the loads on the actual beam.
- Read more about Conjugate Beam Method | Beam Deflection
- Log in or register to post comments