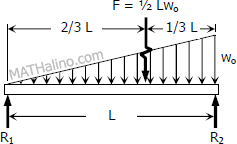
$\Sigma M_{R_2} = 0$
$LR_1 = \frac{1}{3} LF$
$R_1 = \frac{1}{3}\,( \, \frac{1}{2}Lw_o \, )$
$R_1 = \frac{1}{6} Lw_o$
$\Sigma M_{R_1} = 0$
$LR_2 = \frac{2}{3} LF$
$R_2 = \frac{2}{3} \, ( \, \frac{1}{2} Lw_o \, )$
$R_2 = \frac{1}{3} Lw_o$
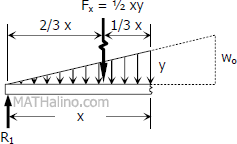 $\dfrac{y}{x} = \dfrac{w_o}{L}$
$\dfrac{y}{x} = \dfrac{w_o}{L}$
$y = \dfrac{w_o}{L}x$
$F_x = \frac{1}{2} xy = \frac{1}{2}x \left( \dfrac{w_o}{L}x \right)$
$F_x = \dfrac{w_o}{2L}x^2$
$V = R_1 - F_x$
$V = \frac{1}{6} Lw_o - \dfrac{w_o}{2L}x^2$
$M = R_1x - F_x\,(\frac{1}{3}x)$
$M = \frac{1}{6}Lw_ox - \dfrac{w_o}{2L}x^2\,(\frac{1}{3}x)$
$M = \frac{1}{6}Lw_ox - \dfrac{w_o}{6L}x^3$
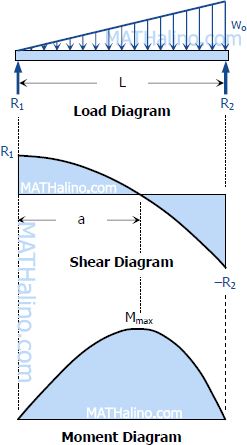 To draw the Shear Diagram:
To draw the Shear Diagram:
V = 1/6 Lwo - wox2/2L is a second degree curve; at x = 0, V = 1/6 Lwo = R1; at x = L, V = -1/3 Lwo = -R2; If a is the location of zero shear from left end, 0 = 1/6 Lwo - wox2/2L, x = 0.5774L = a; to check, use the squared property of parabola:
a2/R1 = L2/(R1 + R2)
a2/(1/6 Lwo) = L2/(1/6 Lwo + 1/3 Lwo)
a2 = (1/6 L3wo)/(1/2 Lwo) = 1/3 L2
a = 0.5774L
To draw the Moment Diagram:
M = 1/6 Lwox - wox3/6L is a third degree curve; at x = 0, M = 0; at x = L, M = 0; at x = a = 0.5774L, M = Mmax.
Mmax = 1/6 Lwo(0.5774L) - wo(0.5774L)3/6L
Mmax = 0.0962L2wo - 0.0321L2wo
Mmax = 0.0641L2wo
