Solution to Problem 419 | Shear and Moment Diagrams

$9R_1 = 5(810)$

$R_1 = 450 \, \text{lb}$
 

$\Sigma M_A = 0$

$9R_2 = 4(810)$

$R_2 = 360 \, \text{lb}$
 

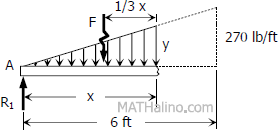Segment AB:
$\dfrac{y}{x} = \dfrac{270}{6}$

$y = 45x$
 

$F = \frac{1}{2}xy = \frac{1}{2}x(45x)$

$F = 22.5x^2$
 

$V_{AB} = R_1 - F$

$V_{AB} = 450 - 22.5x^2 \, \text{lb}$
 

$M_{AB} = R_1x - F(\frac{1}{3}x)$

$M_{AB} = 450x - 22.5x^2(\frac{1}{3}x)$

$M_{AB} = 450x - 7.5x^3 \, \text{lb}\cdot\text{ft}$
 

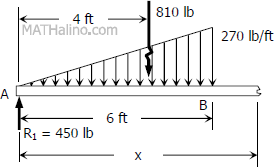Segment BC:
$V_{BC} = 450 - 810$

$V_{BC} = -360 \, \text{lb}$
 

$M_{BC} = 450x - 810(x - 4)$

$M_{BC} = 450x - 810x + 3240$

$M_{BC} = 3240 - 360x \, \text{lb}\cdot\text{ft}$
 

To draw the Shear Diagram:

1. V_AB = 450 - 22.5x² is a second degree curve; at x = 0, V_AB = 450 lb; at x = 6 ft, V_AB = -360 lb.
2. At x = a, V_AB = 0,

   450 - 22.5x² = 0
   22.5x² = 450
   x² = 20
   x = √20

   To check, use the squared property of parabola.

   a²/450 = 62/(450 + 360)
   a² = 20
   a = √20

3. V_BC = -360 lb is constant.

To draw the Moment Diagram:

1. M_AB = 450x - 7.5x³ for segment AB is third degree curve; at x = 0, M_AB = 0; at x = √20, M_AB = 1341.64 lb·ft; at x = 6 ft, M_AB = 1080 lb·ft.
2. M_BC = 3240 - 360x for segment BC is linear; at x = 6 ft, M_BC = 1080 lb·ft; at x = 9 ft, M_BC = 0.