Thin-walled Pressure Vessels

A tank or pipe carrying a fluid or gas under a pressure is subjected to tensile forces, which resist bursting, developed across longitudinal and transverse sections.
 

TANGENTIAL STRESS, σ_t (Circumferential Stress)
Consider the tank shown being subjected to an internal pressure p. The length of the tank is L and the wall thickness is t. Isolating the right half of the tank:
 

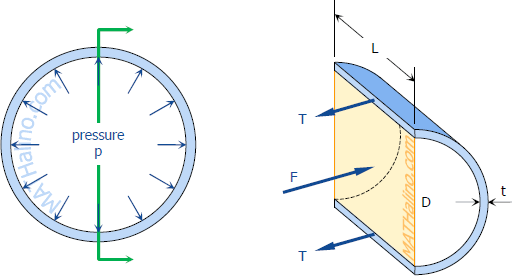
The forces acting are the total pressures caused by the internal pressure p and the total tension in the walls T.
$F = pA = pDL$

$T = \sigma_t A_{wall} = \sigma_t \, tL$
 

$\Sigma F_H = 0$

$F = 2T$

$pDL = 2(\sigma_t \, tL)$

If there exist an external pressure p_o and an internal pressure p_i, the formula may be expressed as:

LONGITUDINAL STRESS, σ_L
Consider the free body diagram in the transverse section of the tank:
 

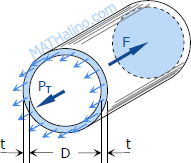
The total force acting at the rear of the tank F must equal to the total longitudinal stress on the wall P_T = σ_LA_wall. Since t is so small compared to D, the area of the wall is close to πDt
$F = pA = p\dfrac{\pi}{4} D^2$

$P_T = \sigma_L \pi Dt$
 

$\Sigma F_H = 0$

$P_T = F$

$\sigma_L \, \pi Dt = p\dfrac{\pi}{4} D^2$

If there exist an external pressure p_o and an internal pressure p_i, the formula may be expressed as:

It can be observed that the tangential stress is twice that of the longitudinal stress.

SPHERICAL SHELL
 

If a spherical tank of diameter D and thickness t contains gas under a pressure of p = p_i - p_o, the stress at the wall can be expressed as: