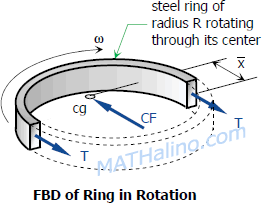
Centrifugal Force, CF:
$CF = M \, \omega^2 \, \bar x$
where:
$M = \dfrac{W}{g} \ \dfrac{\gamma V}{g} = \dfrac{\gamma \pi RA}{q}$
$\omega = v/R$
$\bar x = 2R/\pi$
Thus,
$CF = \dfrac{\gamma \pi RA}{q} \left( \dfrac{v}{R} \right)^2 \left( \dfrac{2R}{\pi} \right)$
$CF = \dfrac{2\gamma A v^2}{g}$
$2T = CF$
$2\gamma A = \dfrac{2\gamma A v^2}{g}$
$\sigma = \dfrac{\gamma \, v^2}{g}$
From the given data:
$\sigma = 20 \, \text{ksi} = (20\,000 \, \text{lb/in}^2)(12 \, \text{in/ft})a^2$
$\sigma = 2\,880\,000 \, \text{lb/ft}^2$
$\gamma = 490 \, \text{lb/ft}^3$
$2\,880\,000 = \dfrac{490v^2}{32.2}$
$v = 435.04 \, \text{ft/sec}$ answer
When $\sigma = 30 \, \text{ksi}$, and $R = 10 \, \text{in}$
$\sigma = \dfrac{\gamma \, v^2}{g}$
$30\,000(12^2) = \dfrac{490v^2}{32.2}$
$v = 532.81 \, \text{ft/sec}$
$\omega = v/R = \dfrac{532.81}{10/12}$
$\omega = 639.37 \, \text{rad/sec}$
$\omega = \dfrac{639.37 \, \text{rad}}{\text{sec}} \times \dfrac{1 \, \text{rev}}{2\pi \, \text{rad}} \times \dfrac{60 \, \text{sec}}{1 \, \text{min}}$
$\omega = 6,105.54 \, \text{rpm}$ answer
