Solution to Problem 140 Pressure Vessel

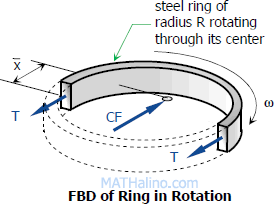
$CF = M \omega^2 \bar x$
 

Where:
$M = \rho V = \rho A \pi R$

$x = 2R / \pi$

 

Thus,
$CF = \rho A \pi R \omega^2 (2R / \pi)$

$CF = 2 \rho A R^2 \omega^2$
 

$2T = CF$

$2 \sigma A = 2 \rho A R^2 \omega^2$

$\sigma = \rho R^2 \omega^2$
 

From the given (Note: 1 N = 1 kg·m/sec²):
$\sigma = 150 \, \text{MPa}$

$\sigma = 150\,000\,000 \, \text{kg} \cdot \text{m/sec}^2 \cdot \text{m}^2$

$\sigma = 150\,000\,000 \, \text{kg/m} \cdot \text{sec}^2$

$\rho = 7.85 \, \text{Mg/m}^3 = 7850 \, \text{kg/m}^3$

$R = 220 \, \text{mm} = 0.22 \, \text{m}$
 

Therefore,
$150\,000\,000 = 7850(0.22)^2 \, \omega^2$

$\omega = 628.33 \, \text{rad/sec}$           answer