$\sigma_t = 6000 \, \text{psi} = 6000 \, \text{lb/in}^2 \, (12 \, \text{in/ft})^2$
$\sigma_t = 864\,000 \, \text{lb/ft}^2$
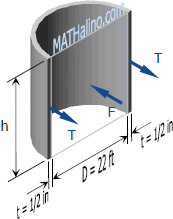Assuming pressure distribution to be uniform:
$p = \gamma h = 62.4h$
$F = pA = 62.4h(Dh)$
$F = 62.4(22)h^2$
$F = 1372.8h^2$
$T = \sigma_t \, A_t = 864\,000(th)$
$T = 864\,000 (\frac{1}{2} \times \frac{1}{12}) \, h$
$T = 36\,000h$
$\Sigma F = 0$
$F = 2T$
$1372.8h^2 = 2(36\,000h)$
$h = 52.45 \, \text{ft}$ answer
COMMENT
Given a free surface of water, the actual pressure distribution on the vessel is not uniform. It varies linearly from zero at the free surface to γh at the bottom (see figure below). Using this actual pressure distribution, the total hydrostatic pressure is reduced by 50%. This reduction of force will take our design into critical situation; giving us a maximum height of 200% more than the h above.
Based on actual pressure distribution:
Total hydrostatic force, F:
$F$ = volume of pressure diagram
$F = \frac{1}{2} (\gamma h^2)D = \frac{1}{2} (62.4h^2)(22)$
$F = 686.4h^2$
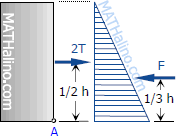$\Sigma M_A = 0$
$2T (\frac{1}{2} \, h) - F (\frac{1}{3} \, h) = 0$
$T = \frac{1}{3} F$
$\sigma_t (ht) = \frac{1}{3} (686.4h^2)$
$h = \dfrac{3\sigma_t \, t}{686.4} = \dfrac{3(864\,000)(\frac{1}{2} \times \frac{1}{12})}{686.4}$
$h = 157.34 \, \text{ft}$
