Spherical Segment

Spherical segment is a solid bounded by two parallel planes through a sphere. In terms of spherical zone, spherical segment is a solid bounded by a zone and the planes of a zone's bases.
 

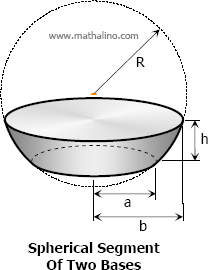
Properties of Spherical Segment

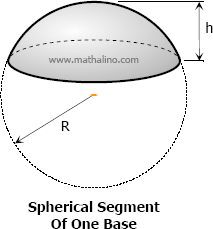
• The bases of a spherical segment are the sections made by the parallel planes. The radii of the lower and upper sections are denoted by a and b, respectively. If either a or b is zero, the segment is of one base. If both a and b are zero, the solid is the whole sphere.
• If one of the parallel planes is tangent to the sphere, the solid thus formed is a spherical segment of one base.
• The spherical segment of one base is also called spherical cap and the two bases is also called spherical frustum.
• The altitude of the spherical segment is the perpendicular distance between the bases. It is denoted by h.

Formulas for Spherical Segment

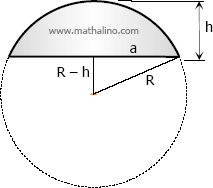The formula for the volume of one base can be derived from volume of two bases with b = 0. Consider the following diagram:
 
$a^2 + (R - h)^2 = R^2$

$a^2 + (R^2 - 2Rh + h^2) = R^2$

$a^2 = 2Rh - h^2$
 

Substitute a² = 2Rh - h² and b = 0 to the formula of spherical segment of two bases

$V = \frac{1}{6}\pi h(3a^2 + 3b^2 + h^2)$

$V = \frac{1}{6}\pi h \, [ \, 3(2Rh - h^2) + 3(0^2) + h^2 \, ]$

$V = \frac{1}{6}\pi h \, [ \, 6Rh - 3h^2 + h^2 \, ]$

$V = \frac{1}{6}\pi h \, [ \, 6Rh - 2h^2 \, ]$

$V = \frac{1}{6}\pi h (2h) [ \, 3R - h \, ]$

$V = \frac{1}{3}\pi h^2 (3R - h)$       (okay!)
 

Note also that the volume of segment of a sphere of altitude h and radii a and b is equal to the volume of a sphere of radius h/2 plus the sum of the volumes of two cylinders whose altitudes are h/2 and whose radii are a and b, respectively.