For θ that is less than 90°
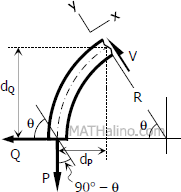Components of Q and P:
$Q_x = Q \sin \theta$
$Q_y = Q \cos \theta$
$P_x = P \sin (90^\circ - \theta)$
$P_x = P \, (\sin 90^\circ \, \cos \theta - \cos 90^\circ \, \sin \theta)$
$P_x = P \, \cos \theta$
$P_y = P \cos (90^\circ - \theta)$
$P_y = P \, (\cos 90^\circ \, \cos \theta + \sin 90^\circ \sin \theta)$
$P_y = P \sin \theta$
Shear:
$V = \Sigma F_y$
$V = Q_y - P_y$
$V = Q \cos \theta - P \sin \theta$ answer
Moment arms:
$d_Q = R \sin \theta$
$d_P = R - R \cos \theta$
$d_P = R \, (1 - \cos \theta)$
Moment:
$M = \Sigma M_{counterclockwise} - \Sigma M_{clockwise}$
$M = Q(d_Q) - P(d_P)$
$M = QR \sin \theta - PR(1 - \cos \theta)$ answer
For θ that is greater than 90°
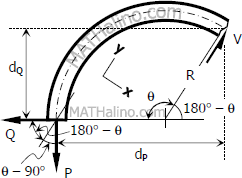Components of Q and P:
$Q_x = Q \sin (180^\circ - \theta)$
$Q_x = Q \, (\sin 180^\circ \cos \theta - \cos 180^\circ \sin \theta)$
$Q_x = Q \cos \theta$
$Q_y = Q \cos (180^\circ - \theta)$
$Q_y = Q (\cos 180^\circ \cos \theta + \sin 180^\circ \sin \theta)$
$Q_y = -Q \sin \theta$
$P_x = P \sin (\theta - 90^\circ)$
$P_x = P (\sin \theta \cos 90^\circ - \cos \theta \sin 90^\circ)$
$P_x = -P \cos \theta$
$P_y = P \cos (\theta - 90^\circ)$
$P_y = P (\cos \theta \cos 90^\circ + \sin \theta \sin 90^\circ)$
$P_y = P \sin \theta$
Shear:
$V = \Sigma F_y$
$V = -Q_y - P_y$
$V = -(-Q \sin \theta) - P \sin \theta$
$V = Q \sin \theta - P \sin \theta$ answer
Moment arms:
$d_Q = R \sin (180^\circ - \theta)$
$d_Q = R (\sin 180^\circ \cos \theta - \cos 180^\circ \sin \theta)$
$d_Q = R \sin \theta$
$d_P = R + R \cos (180^\circ - \theta)$
$d_P = R + R (\cos 180^\circ \cos \theta + \sin 180^\circ \sin \theta)$
$d_P = R - R \cos \theta$
$d_P = R(1 - \cos \theta)$
Moment:
$M = \Sigma M_{counterclockwise} - \Sigma M_{clockwise}$
$M = Q(d_Q) - P(d_P)$
$M = QR \sin \theta - PR(1 - \cos \theta)$ answer
