Application of Double Integration and Superposition Methods to Restrained Beams
Superposition Method
There are 12 cases listed in the method of superposition for beam deflection.
- Cantilever beam with...
- concentrated load at the free end.
- concentrated load anywhere on the beam.
- uniform load over the entire span.
- triangular load with zero at the free end
- moment load at the free end.
- Simply supported beam with...
- concentrated load at the midspan.
- concentrated load anywhere on the beam span.
- uniform load over the entire span.
- triangular load which is zero at one end and full at the other end.
- triangular load with zero at both ends and full at the midspan.
- moment load at the right support.
- moment load at the left support.
See beam deflection by superposition method for details.
Solution to Problem 422 | Shear and Moment Equations
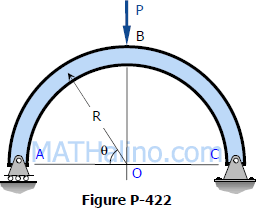
Problem 422
Write the shear and moment equations for the semicircular arch as shown in Fig. P-422 if (a) the load P is vertical as shown, and (b) the load is applied horizontally to the left at the top of the arch.
Shear and Moment Diagrams
Shear and Moment Diagrams
Consider a simple beam shown of length L that carries a uniform load of w (N/m) throughout its length and is held in equilibrium by reactions R1 and R2. Assume that the beam is cut at point C a distance of x from he left support and the portion of the beam to the right of C be removed. The portion removed must then be replaced by vertical shearing force V together with a couple M to hold the left portion of the bar in equilibrium under the action of R1 and wx.
- Read more about Shear and Moment Diagrams
- Log in to post comments