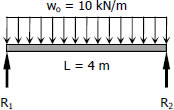
Total Load,
$W = 5(2 \times; 4)$
$W = 40 \, \text{kN}$
Distributed Load,
$w_o = W/L = 40/4$
$w_o = 10 \, \text{kN/m}$
$R_1 = R_2 = \frac{1}{2}W = \frac{1}{2}(40)$
$R_1 = R_2 = 20 \, \text{kN}$
$M_{max} = R_1(L/2) - 10(L/2)(L/4)$
$M_{max} = 20(4/2) - 10(4/2)(4/4)$
$M_{max} = 20 \, \text{kN}\cdot\text{m}$
$S_{required} = \dfrac{M}{f_b} = \dfrac{20(1000^2)}{120}$
$S_{required} = 166\,666.67 \, \text{mm}^3$
From Appendix B, Table B-2 Properties of Wide-Flange Sections (W Shapes): SI Units, of text book:
| Designation |
Section Modulus |
| W130 × 28 |
167 × 103 mm3 |
| W150 × 24 |
168 × 103 mm3 |
| W200 × 22 |
194 × 103 mm3 |
| W250 × 18 |
179 × 103 mm3 |
Consider W250 × 18 with S = 179 × 103 mm3
Checking:
$S_{resisting} \ge S_{live-load} + S_{dead-load}$
$S_{resisting} = 179 \times 10^3 \, \text{mm}^3$
$S_{live-load} = 166\,666.67 \, \text{mm}^3$
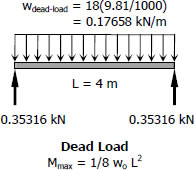
$S_{dead-load} = \dfrac{M_{dead-load}}{f_b} = \dfrac{[\frac{1}{8}[ \, 0.17658)(4 ) \, ] \, 1000}{120}$
$S_{dead-load} = 2.943 \, \text{mm}^3$
$(179 \times 10^3) \ge 166\,666.67 + 2.943$
$(179 \times 10^3) \ge (166.67 \times 10^3)$ (okay!)
Use W250 × 18 for B-1. answer
