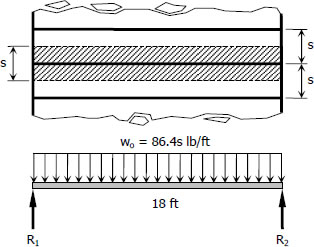
$w_o = (0.6 \, \text{lb/in}^2)(12 \, \text{in/ft})^2(s \, \text{ft})$
$w_o = 86.4s \, \text{lb/ft}$
$R_1 = R_2 = \frac{1}{2}(86.4s)(18)$
$R_1 = R_2 = 777.6s \, \text{lb}$
$M_{max} = 777.6s(9) - 86.4s(9)(4.5)$
$M_{max} = 3499.2s \, \text{lb}\cdot\text{ft}$
From Table B-7 in Appendix B of textbook: Properties of Wide-Flange Sections (W-Shapes): US Customary Units.
| Designation |
Section Modulus, S |
| W10 × 30 |
32.4 in3 |
$f_b = \dfrac{M}{S}$
$18\,000 = \dfrac{3499.2s(12)}{32.4}$
$s = 13.9 \, \text{ft}$ answer
