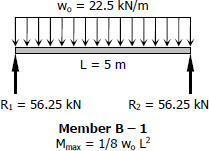
For Member B - 1
$S_{required} = \dfrac{M}{f_b} = \dfrac{\frac{1}{8}(22.5)(5^2)(1000^2)}{120}$
$S_{required} = 586 \times 10^3 \, \text{mm}^3$
From Appendix B, Table B-2 Properties of Wide-Flange Sections (W Shapes): SI Units, of text book:
Use W410 × 39 with S = 634 × 103 mm3 for member B - 1. answer
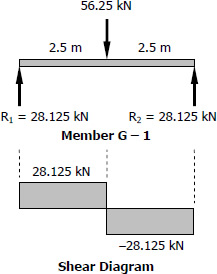For Member G - 1
$M = 2.5(28.125)$
$M = 70.3125 \, \text{kN}\cdot\text{m}$
$S_{required} = \dfrac{M}{f_b} = \dfrac{70.3125(1000^2)}{120}$
$S_{required} = 586 \times 10^3 \, \text{mm}^3$
From Appendix B, Table B-2 Properties of Wide-Flange Sections (W Shapes): SI Units, of text book:
Use W410 × 39 with S = 634 × 103 mm3 for member G - 1. answer
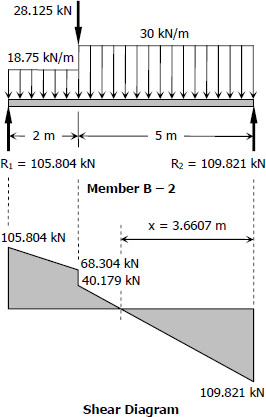For Member B - 2:
$\Sigma M_{R2} = 0$
$7R_1 = 28.125(5) + 18.75(2)(6) + 30(5)(2.5)$
$R_1 = 105.804 \, \text{kN}$
$\Sigma M_{R1} = 0$
$7R_2 = 28.125(2) + 18.75(2)(1) + 30(5)(4.5)$
$R_2 = 109.821 \, \text{kN}$
Location of Maximum Moment:
$\dfrac{x}{109.821} = \dfrac{5 - x}{40.179}$
$40.179x = 549.105 - 109.821x$
$x = 3.6607 \, \text{m}$
Maximum Moment
$M = \frac{1}{2}(3.6607)(109.821)$
$M = 201.01 \, \text{kN}\cdot\text{m}$
$S_{required} = \dfrac{M}{f_b} = \dfrac{201.01(1000^2)}{120}$
$S_{required} = 1\,675 \times 10^3 \, \text{mm}^3$
From Appendix B, Table B-2 Properties of Wide-Flange Sections (W Shapes): SI Units, of text book:
Use W610 × 82 with S = 1 870 × 103 mm3 for member B - 2. answer
For Member B - 3
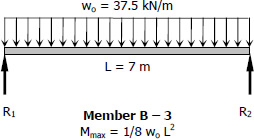$S_{required} = \dfrac{M}{f_b} = \dfrac{\frac{1}{8}(37.5)(7^2)(1000^2)}{120}$
$S_{required} = 1\,914 \times 10^3 \, \text{mm}^3$
From Appendix B, Table B-2 Properties of Wide-Flange Sections (W Shapes): SI Units, of text book:
Use W610 × 92 with S = 2 140 × 103 mm3 for member B - 3. answer
Summary
