Part 1:
$(\,f_b\,)_{max} = \dfrac{Mc}{I}$
where:
$(\,f_b\,)_{max} = 8 \, \text{MPa}$
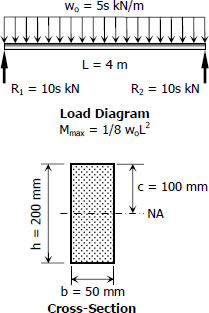
$M = \frac{1}{8}(5s)(4^2)$
$M = 10s \, \text{kN}\cdot\text{m}$
$c = h/2 = 200/2$
$c = 100 \, \text{mm}$
$I = \dfrac{bh^3}{12} = \dfrac{50(200^3)}{12}$
$I = 33.33 \times 10^6 \, \text{mm}^4$
Thus,
$8 = \dfrac{10(100)(1000^2)}{33.33 \times 10^6}$
$s = 0.267 \, \text{m}$ answer
Part 2:
$(\,f_b\,)_{max} = \dfrac{Mc}{I}$
where:
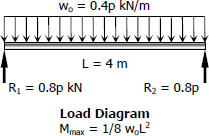
$M = \frac{1}{8}w_o L^2 = \frac{1}{8}(0.4p)(4^2)$
$M = 0.8p$
Thus,
$8 = \dfrac{0.8p(100)(1000^2)}{33.33 \times 10^6}$
$p = 3.33 \, \text{kN/m}^2$ answer
