For Beams (B - 2) | Solution to Problem 542
For Beams (B - 2)
 $\Sigma M_{R2} = 0$
$\Sigma M_{R2} = 0$
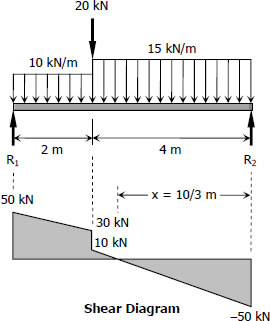
$6R_1 = 20(4) + 10(2)(5) + 15(4)(2)$
$R_1 = 50 \, \text{kN}$
$\Sigma M_{R1} = 0$
$6R_2 = 20(2) + 10(2)(1) + 15(4)(4)$
$R_2 = 50 \, \text{kN}$
Location of Maximum Moment
$\dfrac{x}{50} = \dfrac{4 - x}{10}$
$10x = 200 - 50x$
$x = \frac{10}{3} \, \text{m}$
$M_{max} = \frac{1}{2}(\frac{10}{3})(50)$
$M_{max} = \frac{250}{3} \, \text{kN}\cdot\text{m}$
$S_{required} = \dfrac{M}{f_b} = \dfrac{\frac{250}{3}(1000^2)}{120}$
$S_{required} = 695 \times 10^3 \, \text{mm}^3$
From Appendix B, Table B-2 Properties of Wide Flange Sections (W Shapes): SI Units, of text book:
| Designation | Section Modulus |
| W200 × 71 | 709 × 103 mm3 |
| W250 × 67 | 806 × 103 mm3 |
| W310 × 52 | 747 × 103 mm3 |
| W360 × 51 | 796 × 103 mm3 |
| W410 × 46 | 773 × 103 mm3 |
Consider W410 × 46 with S = 773 × 103 mm3
Checking:
 $S_{supplied} \ge S_{required} + S_{own-weight}$
$S_{supplied} \ge S_{required} + S_{own-weight}$
$S_{supplied} = 773 \times 10^3 \, \text{mm}^3$
$S_{required} = 695 \times 10^3 \, \text{mm}^3$
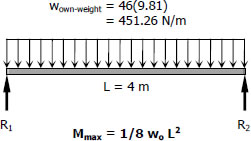
$S_{own-weight} = \dfrac{M_{own-weight}}{f_b} = \dfrac{\frac{1}{8}(451.26)(4^2)(1000)}{12}$
$S_{own-weight} = 7521 \, \text{mm}^3$
$S_{required} + S_{own-weight} = (695 \times 10^3) + 7521$
$S_{required} + S_{own-weight} = 702\,521 \, \text{mm}^3$
$(S_{supplied} = 773 \times 10^3 \, \text{mm}^3) \gt 702\,521 \, \text{mm}^3 \,\, $(ok!)
Use W410 × 46 for Beams (B - 2). answer
Solution for Beams (B - 1)
Solution for Girder (G - 1)
Solution for Beams (B - 2)
Solution for Beams (B - 3)
Solution for Girders (G - 2)

Why only use 4m when solving
Why only use 4m when solving for SDL?