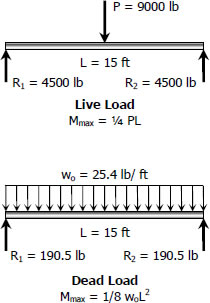
$S_{required} \ge \dfrac{M_{live-load}}{(\,f_b\,)_{max}} \ge \dfrac{\frac{1}{4}(9000)(15)(12)}{18\,000}$
$S_{required} \ge 22.5 \, \text{in}^3$
From Appendix B, Table B-8 Properties of I-Beam Sections (S Shapes): US Customary Units, of text book: Use S10 × 25.4 with S = 24.7 in3. answer
Checking:
$S_{resisting} \ge S_{live-load} + S_{dead-load}$
$S_{live-load} = 22.5 \, \text{in}^3$
$S_{dead-load} = \dfrac{\frac{1}{8}(25.4)(15^2)(12)}{18\,000}$
$S_{dead-load} = 0.48 \, \text{in}^3$
$S_{live-load} + S_{dead-load} = 22.5 + 0.48$
$S_{live-load} + S_{dead-load} = 22.98 \, \text{in}^3$
$(S_{resisting} = 24.7 \, \text{in}^3) \gt 22.98 \, \text{in}^3$ (okay!)
Actual bending moment:
$M = M_{live-load} + M_{dead-load}$
$M = \frac{1}{4} PL + \frac{1}{8}w_oL^2$
$M = \frac{1}{4}(9000)(15) + \frac{1}{8}(25.4)(152)$
$M = 34,464.38 \, \text{lb}\cdot\text{ft}$
Actual stress:
$(\,f_b\,)_{max} = \dfrac{M}{S} = \dfrac{34,464.38(12)}{24.7}$
$(\,f_b\,)_{max} = 16,743.83 \, \text{psi}$
$(\,f_b\,)_{max} = 16.74 \, \text{ ksi}$ answer
