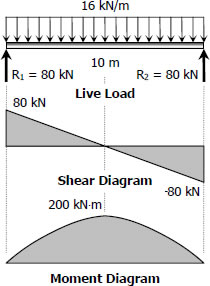
$S_{required} \ge \dfrac{M_{live-load}}{(\,f_b\,)_{max}} \ge \dfrac{200(1000^2)}{120}$
$S_{required} \ge 1,666,666.67 \, \text{mm}^3$
$S_{required} \ge 1,666.67 \times 10^3 \, \text{mm}^3$
Starting at the bottom of Appendix B, Table B-2 Properties of Wide-Flange Sections (W Shapes): SI Units, of text book, the following are the first to exceed the S above:
| Designation |
Section Modulus |
| W250 × 149 |
1,840 × 103 mm3 |
| W310 × 118 |
1,750 × 103 mm3 |
| W360 × 101 |
1,690 × 103 mm3 |
| W410 × 100 |
1,920 × 103 mm3 |
| W460 × 89 |
1,770 × 103 mm3 |
| W530 × 85 |
1,810 × 103 mm3 |
| W610 × 82 |
1,870 × 103 mm3 |
| W690 × 125 |
3,500 × 103 mm3 |
Use the lightest section W610 × 82. answer
Checking:
$S_{resisting} \ge S_{live-load} + S_{dead-load}$
$S_{live-load} = 1\,666.67 \times 10^3 \, \text{mm}^3$
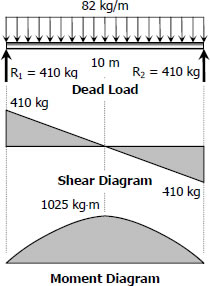
$S_{dead-load} = \dfrac{1025(9.81)(1000)}{120}$
$S_{dead-load} = 83.79 \times 10^3 \, \text{mm}^3$
$S_{live-load} + S_{dead-load} = (1\,666.67 \times 10^3) + (83.79 \times 10^3)$
$S_{live-load} + S_{dead-load} = 1 750.46 \times 10^3 \, \text{mm}^3$
The resisting S of W610 × 82 is 1,870 × 103 mm3, the S due to live-load and dead-load is only 1,750.46 × 103 mm3, therefore, the chosen section is sufficient to resist the combined dead-load and live-load.
Actual bending moment due to dead and live loads:
$M = M_{live-load} + M_{dead-load}$
$M = 200 + 1025(9.81/1000)$
$M = 210.06 \, \text{kN}\cdot\text{m}$
Actual stress:
$(\,f_b\,)_{max} = \dfrac{M}{S} = \dfrac{210.06(1000^2)}{1870 \times 10^3}$
$(\,f_b\,)_{max} = 112.33 \, \text{ MPa}$ answer
