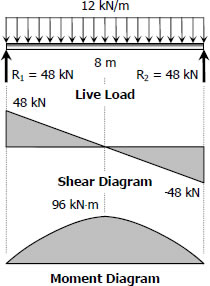
$S_{required} \ge \dfrac{M_{live-load}}{(\,f_b\,)_{max}} \ge \dfrac{96(1000^2)}{120}$
$S_{required} \ge 800 \times 10^3 \, \text{mm}^3$
From Appendix B, Table B-2 Properties of Wide-Flange Sections (W Shapes): SI Units, of text book:
| Designation |
Section Modulus |
| W200 × 86 |
853 × 103 mm3 |
| W250 × 67 |
806 × 103 mm3 |
| W310 × 60 |
849 × 103 mm3 |
| W360 × 57 |
897 × 103 mm3 |
| W410 × 54 |
924 × 103 mm3 |
| W460 × 52 |
943 × 103 mm3 |
Use the lightest section W460 × 52. answer
 Checking:
Checking:
$S_{resisting} \ge S_{live-load} + S_{dead-load}$
$S_{live-load} = 800 \times 10^3 \, \text{mm}^3$
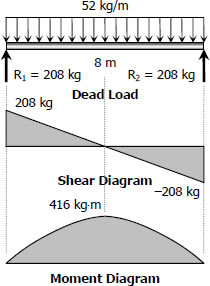
$S_{dead-load} = \dfrac{416(9.81)(1000)}{120}$
$S_{dead-load} = 34 \times 10^3 \, \text{mm}^3$
$S_{live-load} + S_{dead-load} = (800 \times 10^3) + (34 \times 10^3)$
$S_{live-load} + S_{dead-load} = 834 \times 10^3 \, \text{mm}^3$
$(943 \times 10^3 \, \text{mm}^3) > (834 \times 10^3 \, \text{mm}^3)$ (okay!)
Actual bending moment:
$M = M_{live-load} + M_{dead-load}$
$M = 96 + 416(9.81/1000) = 100.08 \, \text{kN}\cdot\text{m}$
Actual stress:
$(\,f_b\,)_{max} = \dfrac{M}{S} = \dfrac{100.08(1000^2)}{943 \times 10^3}$
$(\,f_b\,)_{max} = 106.13 \, \text{ MPa}$ answer
