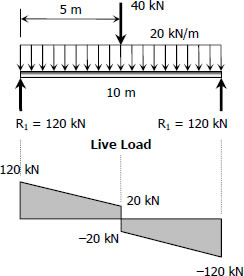
$M_{live-laod} = \frac{1}{2}(120 + 20)(5)$
$M_{live-laod} = 350 \, \text{kN}\cdot\text{m}$
$S_{required} \ge \dfrac{M_{live-load}}{(\,f_b\,)_{max}} \ge \dfrac{350(1000^2)}{120}$
$S_{required} \ge 2\,916.67 \times 10^3 \, \text{mm}^3$
From Appendix B, Table B-2 Properties of Wide-Flange Sections (W Shapes): SI Units, of text book:
| Designation |
Section Modulus |
| W310 × 202 |
3 050 × 103 mm3 |
| W360 × 179 |
3 120 × 103 mm3 |
| W460 × 144 |
3 080 × 103 mm3 |
| W530 × 138 |
3 140 × 103 mm3 |
| W610 × 125 |
3 220 × 103 mm3 |
| W690 × 125 |
3 500 × 103 mm3 |
W610 × 125 has a theoretical mass of 125.1 kg/m while W690 × 125 has a theoretical mass of 125.6 kg/m. Thus, use W610 × 125 with S = 3 220 × 103 mm3. answer
Checking:
$S_{resisting} \ge S_{live-load} + S_{dead-load}$
$S_{live-load} = 2\,916.67 \times 10^3 \, \text{mm}^3$
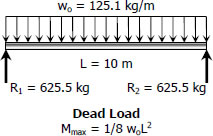
$S_{dead-load} = \dfrac{\frac{1}{8}(125.1)(9.81)(10^2)(1000)}{120}$
$S_{dead-load} = 127.84 \times 10^3 \, \text{mm}^3$
$S_{live-load} + S_{dead-load} = (2\,916.67 \times 10^3) + (127.84 \times 10^3)$
$S_{live-load} + S_{dead-load} = 3\,044.51 \times 10^3 \, \text{mm}^3$
$(S_{resisting} = 3\,220 \times 10^3 \, \text{mm}^3) > 3\,044.4 \times 10^3 \, \text{ mm}^3$ (okay!)
