$2x^2 + 4x + y = 0$
$2(x^2 + 2x + 1) = -y + 2(1)$
$2(x + 1)^2 = -(y - 2)$
$(x + 1)^2 = -\frac{1}{2}(y - 2)$ → downward parabola, vertex at (-1, 2), LR = 1/2
Points of intersection
$2x^2 + 4x + 2x = 0$
$2x(x + 3) = 0$
$x = 0 \, \text{ and } -3$
when x = 0, y = 2(0) = 0
when x = -3, y = 2(-3) = -6
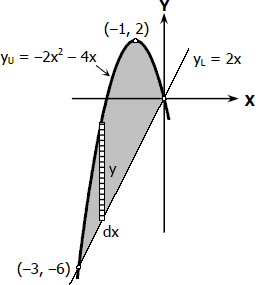
points of intersection: (0, 0) and (-3, -6)
$A = \displaystyle{{\int_{x_1}}^{x_2}} y \, dx$
$A = \displaystyle{{\int_{x_1}}^{x_2}} (y_U - y_L) \, dx$
$A = \displaystyle{{\int_{-3}}^0} [ \, (-2x^2 - 4x) - 2x \, ] \, dx$
$A = -2\displaystyle{{\int_{-3}}^0} (2x^2 + 3x) \, dx$
$A = -2 \left[ \dfrac{2x^3}{3} + \dfrac{3x^2}{2} \right]_{-3}^0$
$A = -2 \left[ \dfrac{2(0)^3}{3} + \dfrac{3(0)^2}{2} \right] + 2 \left[ \dfrac{2(-3)^3}{3} + \dfrac{3(-3)^2}{2} \right]$
$A = -2 [ \, 0 \, ] + 2 [ \, \frac{9}{2} \, ]$
$A = 9 \, \text{ unit}^2$ answer
