Solution to Problem 455 | Moving Loads

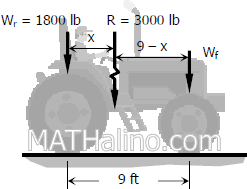
$R = W_r + W_f$

$3000 = 1800 + W_f$

$W_f = 1200 \, \text{lb}$
 

$Rx = 9W_f$

$3000x = 9(1200)$

$x = 3.6 \, \text{ft}$

$9 - x = 5.4 \, \text{ft}$
 

 

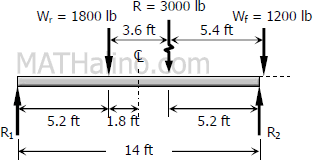When the midspan is midway between W_r and R, the front wheel W_f will be outside the span (see figure). In this case, only the rear wheel W_r = 1800 lb is the load. The maximum moment for this condition is when the load is at the midspan.
$R_1 = R_2 = \frac{1}{2}(1800)$

$R_1 = 900 \, \text{lb}$
 

 

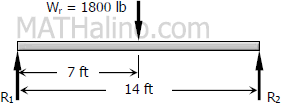Maximum moment under W_r
$M_{To\,\,the\,\,left\,\,of\,\,rear\,\,wheel} = 7R_1$

$M_{To\,\,the\,\,left\,\,of\,\,rear\,\,wheel} = 7(900)$

$M_{To\,\,the\,\,left\,\,of\,\,rear\,\,wheel} = 6300 \, \text{lb}\cdot\text{ft}$
 

 

Maximum moment under W_f
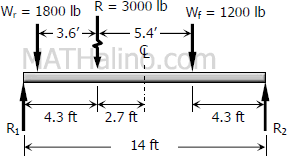$\Sigma M_{R1} = 0$
$14R_2 = 4.3R$
$14R_2 = 4.3(3000)$
$R_2 = 921.43 \, \text{lb}$
 

$M_{To\,\,the\,\,right\,\,of\,\,front\,\,wheel} = 4.3R_2$

$M_{To\,\,the\,\,right\,\,of\,\,front\,\,wheel} = 4.3(921.43)$

$M_{To\,\,the\,\,right\,\,of\,\,front\,\,wheel} = 3962.1 \, \text{lb}\cdot\text{ft}$
 

Thus,
$M_{max} = M_{To\,\,the\,\,left\,\,of\,\,rear\,\,wheel}$

$M_{max} = 6300 \, \text{lb}\cdot\text{ft} \,\,$ answer
 

 

The maximum shear will occur when the rear wheel (wheel of greater load) is directly over the support.
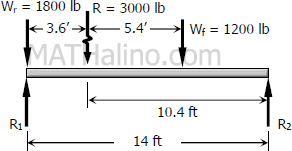$\Sigma M_{R2} = 0$

$14R_1 = 10.4R$

$14R_1 = 10.4(3000)$

$R_1 = 2228.57 \, \text{lb}$
 

Thus,
$V_{max} = 2228.57 \, \text{lb} \,\,$ answer