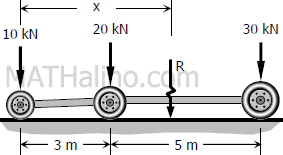
$R = 10 + 20 + 30$
$R = 60 \, \text{kN}$
$xR = 3(20) + 8(30)$
$x(60) = 3(20) + 8(30)$
$x = 5 \, \text{m}$
Maximum moment under 10 kN wheel load
$\Sigma M_{R2} = 0$
$12R_1 = 3.5R$
$12R_1 = 3.5(60)$
$12R_1 = 210$
$R_1 = 17.5 \, \text{kN}$
$M_{To\,the\,left\,of\,10\,kN} = 3.5R_1$
$M_{To\,the\,left\,of\,10\,kN} = 3.5(17.5)$
$M_{To\,the\,left\,of\,10\,kN} = 61.25 \, \text{kN}\cdot\text{m}$
Maximum moment under 20 kN wheel load
$\Sigma M_{R2} = 0$
$12R_1 = 5R$
$12R_1 = 5(60)$
$R_1 = 25 \, \text{kN}$
$M_{To\,the\,left\,of\,20\,kN} = 5R_1 - 3(10)$
$M_{To\,the\,left\,of\,20\,kN} = 5(25) - 30$
$M_{To\,the\,left\,of\,20\,kN} = 95 \text{kN}\cdot\text{m}$
Maximum moment under 30 kN wheel load
When the centerline of the beam is midway between reaction R = 60 kN and 30 kN, the 10 kN comes off the span.
$R = 20 + 30$
$R = 50 \, \text{kN}$
$xR = 5(30)$
$x(50) = 150$
$x = 3 \, \text{m} \,\,$ from 20 kN wheel load
$\Sigma M_{R1} = 0$
$12R_2 = 5R$
$12R_2 = 5(50)$
$R_2 = 20.83 \, \text{kN}$
$M_{To\,\,the\,\,right\,\,of\,\,30\,\,kN} = 5R_2$
$M_{To\,\,the\,\,right\,\,of\,\,30\,\,kN} = 5(20.83)$
$M_{To\,\,the\,\,right\,\,of\,\,30\,\,kN} = 104.17 \, \text{kN}\cdot\text{m}$
Thus, the maximum moment will occur when only the 20 and 30 kN loads are on the span.
$M_{max} = M_{To\,\,the\,\,right\,\,of\,\,30\,\,kN}$
$M_{max} = 104.17 \, \text{ kN}\cdot\text{m}$ answer
Maximum Shear
The maximum shear will occur when the three loads are on the span and the 30 kN load is directly over the support.
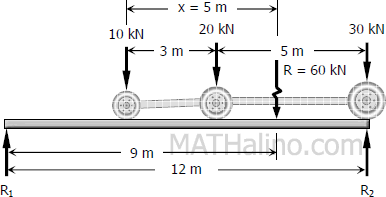$\Sigma M_{R1} = 0$
$12R_2 = 9R$
$12R_2 = 9(60)$
$R_2 = 45 \, \text{kN}$
Thus,
$V_{max} = 45 \, \text{ kN}$ answer
