$h = L_1 \sin 45^\circ$
$h = L_2 \sin 60^\circ$
$h = h$
$L_1 \sin 45^\circ = L_2 \sin 60^\circ$
$L_1 = 1.2247L_2$
$\delta_1 = \delta \sin 45^\circ$
$\delta_2 = \delta \sin 60^\circ$
$\dfrac{\delta_1}{\delta_2} = \dfrac{\delta \sin 45^\circ}{\delta \sin 60^\circ}$
$\delta_1 = 0.8165\delta_2$
$\alpha \, L_1 \, \Delta T + \dfrac{P_1 L_1}{AE} = 0.8165 \, \left[ \, \alpha L_2 \Delta T + \dfrac{P_2 L_2}{AE} \, \right]$
$(11.7 \times 10^{-6})L_1 (50) + \dfrac{P_1 L_1}{600(200\,000)} = 0.8165 \, \left[ \, (11.7 \times 10^{-6}) (50) + \dfrac{P_2 L_2}{600(200\,000)} \, \right]$
$70,200 L_1 + P_1 L_1 = 0.8165(70,200 L_2 + P_2 L_2)$
$(70,200 + P_1)L_1 = 0.8165(70,200 + P_2)L_2$
$(70,200 + P_1)1.2247L_2 = 0.8165(70,200 + P_2)L_2$
$1.5(70,200 + P_1) = 70,200 + P_2$
$P_2 = 1.5P_1 + 35,100$ → Equation (1)
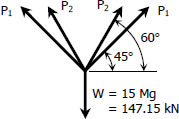$\Sigma F_V = 0$
$2(P_1 \sin 45^\circ) + 2(P_2 \sin 60^\circ) = 147.15(1000)$
$P_1 \sin 45^\circ + P_2 \sin 60^\circ = 72,575$
$P_1 \sin 45^\circ + (1.5P_1 + 35,100) \sin 60^\circ = 72,575$
$0.7071P_1 + 1.299P_1 + 30,397.49 = 72,575$
$2.0061P_1 = 42,177.51$
$P_1 = 21,024.63 \, \text{N}$
$P_2 = 1.5(21,024.63) + 35,100$
$P_2 = 66,636.94 \, \text{N}$
$P_A = P_D = P_1 = 21.02 \, \text{kN}$ answer
$P_B = P_C = P_2 = 66.64 \, \text{kN}$ answer
