Internal pressure of aluminum tube to cause contact with the steel:
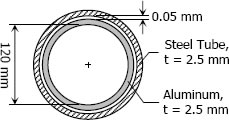 $\delta_{al} = \left( \dfrac{\sigma \, L}{E} \right)_{al}$
$\delta_{al} = \left( \dfrac{\sigma \, L}{E} \right)_{al}$
$\pi (122.6 - 122.5) = \dfrac{\sigma_1 \, (122.5 \pi)}{70\,000}$
$\sigma_1 = 57.143 \, \text{MPa}$
$\dfrac{p_1 \, D}{2t} = 57.143$
$\dfrac{p_1 (120)}{2(2.5)} = 57.143$
$p_1 = 2.381 \, \text{ MPa}$ → pressure that causes aluminum to contact with the steel, further increase of pressure will expand both aluminum and steel tubes.
Let pc = contact pressure between steel and aluminum tubes
$2P_{st} + 2P_{al} = F$
$2P_{st} + 2P_{al} = 5.0(120.1)(1)$
$P_{st} + P_{al} = 300.25$ → Equation (1)
The relationship of deformations is (from the figure):
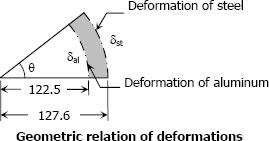 $\delta_{st} = 127.6 \theta$
$\delta_{st} = 127.6 \theta$
$\theta = \delta_{st} / 127.6$
$\delta_{al} = 122.5 \theta$
$\delta_{al} = 122.5(\delta_{st} / 127.6)$
$\delta_{al} = 0.96 \, \delta_{st}$
$\left( \dfrac{PL}{AE} \right)_{al} = 0.96 \, \left( \dfrac{PL}{AE} \right)_{st}$
$\dfrac{P_{al} \, (122.5 \pi)}{2.5(70\,000)} = 0.96 \, \left[ \dfrac{P_{st} \, (127.6 )}{2.5(200\,000)} \right]$
$P_{al} = 0.35P_{st}$ → Equation (2)
From Equation (1)
$P_{st} + 0.35P_{st} = 300.25$
$P_{st} = 222.41 \, \text{N}$
From Equation (2)
$P_{al} = 0.35(222.41)$
$P_{al} = 77.84 \, \text{N}$
Contact Force
$F_c + 2P_{st} = F$
$p_c (125.1)(1) + 2(77.84) = 5(120.1)(1)$
$p_c = 3.56 \, \text{ MPa}$ answer

My question is how did the
My question is how did the modulus of elasticity (E) is 70000 in Al and 200000 in steel? Ty