Solution to Problem 257 Statically Indeterminate

$L_{AD} = \dfrac{10}{\cos 20^\circ} = 10.64 \, \text{ ft}$
 

$\Sigma F_V = 0$
$P_{AB} \cos 40^\circ + P_{AC} + P_{AD} \cos 20^\circ = 10(1000)$

$0.7660P_{AB} + P_{AC} + 0.9397P_{AD} = 10~000$       → Equation (1)
 

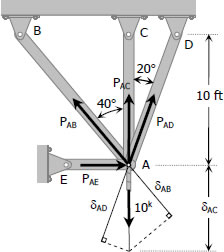$\delta_{AB} = \cos 40^\circ \delta_{AC} = 0.7660 \delta_{AC}$

$\left( \dfrac{PL}{AE} \right)_{AB} = 0.7660 \left( \dfrac{PL}{AE} \right)_{AC}$

$\dfrac{P_{AB} (13.05)}{0.3(29 \times 10^6)} = 0.7660 \left[ \dfrac{P_{AC} (10)}{0.6(10 \times 10^6)} \right]$

$P_{AB} = 0.8511 P_{AC}$       → Equation (2)
 

$\delta_{AD} = \cos 20^\circ \delta_{AC} = 0.9397 \delta_{AC}$

$\left( \dfrac{PL}{AE} \right)_{AD} = 0.9397 \left( \dfrac{PL}{AE} \right)_{AC}$

$\dfrac{P_{AB} (10.64)}{0.3(29 \times 10^6)} = 0.9397 \left[ \dfrac{P_{AC} (10)}{0.6(10 \times 10^6)} \right]$

$P_{AD} = 1.2806 P_{AC}$       → Equation (3)
 

Substitute P_AB of Equation (2) and P_AD of Equation (3) to Equation (1)
$0.7660(0.8511P_{AC}) + P_{AC} + 0.9397(1.2806P_{AC}) = 10\,000$

$2.8553P_{AC} = 10\,000$

$P_{AC} = 3\,502.23 \, \text{ lb}$
 

From Equation (2)
$P_{AB} = 0.8511(3\,502.23)$

$P_{AB} = 2\,980.75 \, \text{ lb }$
 

From Equation (3)
$P_{AD} = 1.2806(3\,502.23)$

$P_{AD} = 4\,484.96 \text{ lb }$
 

Stresses:
$\sigma = P / A$

$\sigma_{AB} = 2980.75 / 0.3 = 9\,935.83 \, \text{ psi}$           answer

$\sigma_{AC} = 3502.23 / 0.6 = 5\,837.05 \, \text{ psi}$           answer

$\sigma_{AD} = 4484.96 / 0.3 = 14\,949.87 \, \text{ psi}$           answer
 

$\Sigma F_H = 0$

$P_{AE} + P_{AD} \sin 20^\circ = P_{AB} \sin 40^\circ$

$P_{AE} = 2\,980.75 \sin 40^\circ - 4\,484.96 \sin 20^\circ$

$P_{AE} = 382.04 \, \text{ lb}$           answer