Moment Diagram by Parts
The moment-area method of finding the deflection of a beam will demand the accurate computation of the area of a moment diagram, as well as the moment of such area about any axis. To pave its way, this section will deal on how to draw moment diagram by parts and to calculate the moment of such diagrams about a specified axis.
Basic Principles
- The bending moment caused by all forces to the left or to the right of any section is equal to the respective algebraic sum of the bending moments at that section caused by each load acting separately.
$M = ( \, \Sigma M \, )_L = ( \, \Sigma M \, )_R$ - The moment of a load about a specified axis is always defined by the equation of a spandrel
$y = kx^n$where n is the degree of power of x.
The graph of the above equation is as shown below
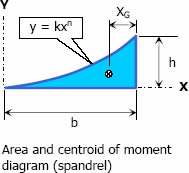
and the area and location of centroid are defined as follows.
Cantilever Loadings
A = area of moment diagram
Mx = moment about a section of distance x
barred x = location of centoid
Degree = degree power of the moment diagram
Couple or Moment Load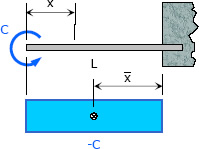 $A = -CL$ $A = -CL$
$M_x = -C$ $\bar x = \frac{1}{2} L$ Degree: zero |
Concentrated Load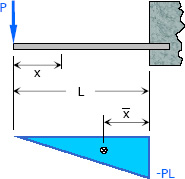 $A = -\frac{1}{2} PL^2$ $A = -\frac{1}{2} PL^2$
$M_x = -Px$ $\bar x = \frac{1}{3} L$ Degree: first |
Uniformly Distributed Load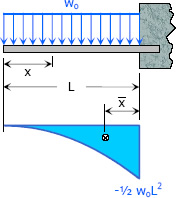 $A = -\frac{1}{6} w_o L^3$ $A = -\frac{1}{6} w_o L^3$
$M_x = -\frac{1}{2} w_o x^2$ $\bar x = \frac{1}{4}L$ Degree: second |
Uniformly Varying Load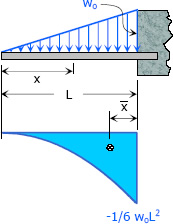 $A = -\frac{1}{24} w_o L^3$ $A = -\frac{1}{24} w_o L^3$
$M_x = -\dfrac{w_o}{6L} x^2$ $x = \frac{1}{5}L$ Degree: third |

Saan po galing yung L sa Mx=
Saan po galing yung L sa Mx=−[wox2]/6L under Uniformly Varying Load?
Pagkaintindi ko po sa moment is
Mx = -1/2 * (wo) * x * (1/3)x = −[wox2]/6
Mali po ang equation mo…
In reply to Saan po galing yung L sa Mx= by Bhong
Mali po ang equation mo. Palitan mo ng $y$ ang $w_o$ sa inyong equation, then i-express mo ang $y$ in terms of $x$ and $w_o$, magawa mo yan by ratio and proportion. Sa equation na nakapost na $M_x = -\dfrac{w_o}{6L}x^2$, try mo palitan ang $x$ ng $L$ and it will make sense, mapapalabas mo kasi ang $M_\text{max}$.