Calculator Technique for Solving Volume Flow Rate Problems in Calculus

The following models of CASIO calculator may work with this method: fx-570ES, fx-570ES Plus, fx-115ES, fx-115ES Plus, fx-991ES, and fx-991ES Plus.
 

The following calculator keys will be used for the solution

Name Key Operation Shift SHIFT Mode MODE

Name Key Operation Stat SHIFT → 1[STAT] AC AC

This is one of the series of post in calculator techniques in solving problems. You may also be interested in my previous posts: Calculator technique for progression problems and Calculator technique for clock problems; both in Algebra.
 

Flow Rate Problem
Water is poured into a conical tank at the rate of 2.15 cubic meters per minute. The tank is 8 meters in diameter across the top and 10 meters high. How fast the water level rising when the water stands 3.5 meters deep.
 

Traditional Solution
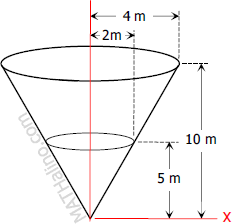
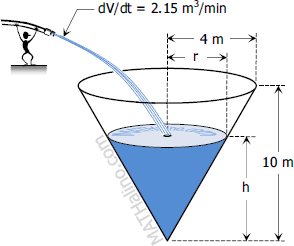$\dfrac{r}{h} = \dfrac{4}{10}$

$r = \frac{2}{5}h$
 

Volume of water inside the tank
$V = \frac{1}{3}\pi r^2 h$

$V = \frac{1}{3}\pi (\frac{2}{5}h)^2 h$

$V = \frac{4}{75}\pi h^3$
 

Differentiate both sides with respect to time
$\dfrac{dV}{dt} = \frac{4}{25}\pi h^2 \dfrac{dh}{dt}$

$2.15 = \frac{4}{25}\pi h^2 \dfrac{dh}{dt}$
 

When h = 3.5 m
$2.15 = \frac{4}{25}\pi (3.5^2) \dfrac{dh}{dt}$

$\dfrac{dh}{dt} = 0.3492 \, \text{m/min}$           answer
 

Solution by Calculator

MODE → 3:STAT → 3:_+cX2
 

AC → 2.15 ÷ 3.5y-caret = 0.3492           answer
 

To input the 3.5y-caret above, do
3.5 → SHIFT → 1[STAT] → 7:Reg → 6:y-caret
 

What we just did was actually v = Q / A which is the equivalent of $\dfrac{dh}{dt} = \dfrac{dV/dt}{A}$ for this problem.
 

Problem
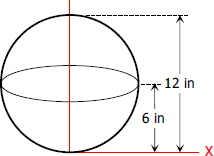
Water is being poured into a hemispherical bowl of radius 6 inches at the rate of x cubic inches per second. Find x if the water level is rising at 0.1273 inch per second when it is 2 inches deep?
 

Traditional Solution
Volume of water inside the bowl
$V = \frac{1}{3}\pi h^2(3r − h)$

$V = \frac{1}{3}\pi h^2 [ \, 3(6) - h \, ]$

$V = \frac{1}{3}\pi (18h^2 - h^3)$
 

Differentiate both sides with respect to time
$\dfrac{dV}{dt} = \frac{1}{3}\pi (36h - 3h^2) \dfrac{dh}{dt}$
 

When h = 2 inches, dh/dt = 0.1273 inch/sec
$\dfrac{dV}{dt} = \frac{1}{3}\pi [ \, 36(2) - 3(2^2) \, ] (0.1273)$

$x = 7.9985 \, \text{in}^3\text{/sec}$           answer
 

Calculator Technique
MODE → 3:STAT → 3:_+cX2
 

AC → 0.1273 × 2y-caret = 7.9985           answer
 

I hope you enjoy this post. Next time you solve problems involving flow rate, try to use this calculator technique to save time.